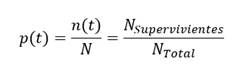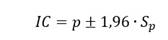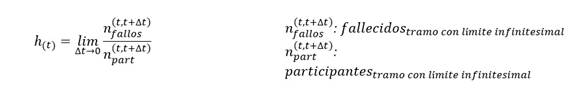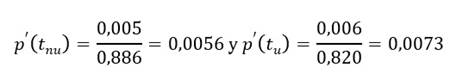Implicaciones prácticas
Políticas de retención estudiantil: Los hallazgos sugieren diseñar políticas más eficaces, enfocadas en estudiantes de hogares con menor nivel educativo, quienes tienen mayor probabilidad de desvinculación.
Atención diferenciada: Dado que el género y la edad de ingreso influyen en las tasas de graduación, se recomienda implementar programas que apoyen a estudiantes mayores y hombres jóvenes, quienes enfrentan más dificultades para graduarse.
Acompañamiento académico personalizado: Las trayectorias más largas están asociadas con mayores tasas de no acreditación, por lo que es importante implementar estrategias de seguimiento temprano para estudiantes en riesgo de retraso.
Diferencias de currículos: Los estudiantes con perfiles más exitosos tienden a elegir carreras más largas y tienen mayores probabilidades de graduarse en menos tiempo. Esto subraya la necesidad de enfocarse especialmente en aquellos con perfiles menos favorecidos que optan por transitar dichas carreras, brindándoles apoyo adicional para mejorar sus tasas de graduación.
Entorno educativo inclusivo: Dado que el nivel educativo del hogar impacta la graduación, es necesario que las instituciones promuevan entornos inclusivos que compensen las desventajas sociales, ofreciendo oportunidades igualitarias a todos los estudiantes.
Introducción
En las ciencias sociales es común buscar la estimación probabilística de eventos específicos, como la desvinculación estudiantil, la obtención de títulos, la movilidad social o el logro de determinados niveles de ingresos. Estos fenómenos son frecuentemente objeto de investigación debido a su relevancia en la comprensión de las dinámicas sociales y educativas. Sin embargo, es menos habitual enfocarse en la estimación de la probabilidad de que dichos eventos ocurran en un momento específico o dentro de un determinado período de tiempo, a pesar de que este enfoque puede ofrecer una visión más precisa y útil en contextos como la educación superior.
Este artículo propone adoptar el análisis de supervivencia como una técnica metodológica clave para estudiar las trayectorias estudiantiles en la educación superior. Este enfoque permite no solo estimar la probabilidad de que ocurra un evento, sino también cuándo es más probable que suceda y qué atributos individuales se observan asociados con dicho acaecimiento. Esto proporciona una herramienta potente para la investigación educativa y la toma de decisiones en este ámbito.
Las revisiones sistemáticas y los antecedentes en el área han brindado una base sólida para estudiar la desvinculación en la educación superior. La teoría de la persistencia y deserción de Tinto ofrece un marco para comprender cómo los factores institucionales y sociales influyen en la permanencia de los estudiantes, lo que sugiere la integración social y académica como clave para mejorar la retención. Otros enfoques, como el de Munizaga et al., abordan factores socioeconómicos y culturales específicos de la realidad latinoamericana, y proporcionan una perspectiva actualizada sobre las causas de la desvinculación estudiantil en contextos particulares. Además, estudios como el de Behr et al. (2020) aportan datos empíricos sobre la efectividad de diversas intervenciones institucionales dirigidas a mejorar la retención.
Revisiones exhaustivas, como las de Munizaga et al. (2018) y Chiarino et al. (2024), han destacado el debate en torno a la temática en América Latina, promovido por la red ALFA-GUIA en el X Congreso CLABES. Donoso y Schiefelbein, siguiendo los desarrollos de Tinto (1987) y Bean (1985), señalan que las creencias influyen en las actitudes de los estudiantes, moldeando sus intenciones conductuales, aunque estos enfoques no abordan explícitamente la toma de decisiones en cuanto a continuar o abandonar los estudios.
No obstante, las investigaciones educativas sobre las trayectorias estudiantiles en educación superior no incorporan una perspectiva teórica que analice la mecánica de la toma de decisiones en función de la evaluación de riesgos, lo que introduce desafíos específicos en el diseño de los modelos estadísticos.
Esto queda en evidencia al examinar los mapas de relación intra e interniveles sistémicos que proponen Chiarino et al. (2024, pp. 24-25), en que, luego de una revisión exhaustiva de la producción reciente, la incorporación de vectores potencialmente explicativos elude justamente algunos factores relevantes, como los indicativos de la influencia del origen de clase en la toma de decisiones, factores esenciales para comprender los procesos desencadenantes de la desvinculación.
En este sentido, Boudon (2006, p. 17) sugiere que los individuos toman decisiones racionales basadas en una evaluación de costos y beneficios. En el contexto educativo, los estudiantes pueden evaluar el riesgo de continuar con sus estudios considerando diversos factores, como el apoyo institucional, la integración social y académica y las oportunidades laborales futuras. Esta evaluación tiene signo y efecto diferente en función de factores específicos como el clima educativo del hogar de origen. En definitiva, se sugiere partir del supuesto de que el riesgo latente de fracaso y la proyección de las metas educativas autoimpuestas influyen categóricamente en la decisión de permanecer o abandonar la educación superior.
Estos elementos proporcionan el contexto en el que los estudiantes evalúan el riesgo y las recompensas asociadas con la continuación de sus estudios. La investigación educativa debe proporcionar datos empíricos sobre qué estrategias y políticas son más efectivas para mejorar la retención estudiantil. Las estrategias pueden ser vistas como opciones que los estudiantes consideran dentro del marco de elecciones racionales, ajustando sus decisiones en función de la percepción de riesgo y beneficio que estas estrategias ofrecen.
El análisis de supervivencia es un instrumento común en estudios de salud, particularmente en epidemiología y biología, en las que se utiliza para medir la esperanza de vida.
A fines del siglo XVII, el matemático y estadístico inglés John Graunt desarrolló las primeras tablas de vida, que mostraban la probabilidad de supervivencia en diferentes edades. A principios del siglo XIX, el actuario y matemático británico Benjamín Gompertz formuló la “ley de vida”, que lleva su nombre. Era una función sigmoidea creada para la Royal Society en 1825 para detallar su ley de mortalidad humana, que muestra que la tasa de mortalidad aumenta exponencialmente con la edad, con un incremento lento al comienzo y al final de un período de tiempo dado.
A mediados del siglo XX, el análisis de supervivencia se consolidó como una herramienta esencial en la investigación del cáncer. Investigadores como Sir Richard Doll y Austin Bradford Hill realizaron estudios que examinaban la supervivencia de pacientes con cáncer y desarrollaron técnicas para analizar datos de tiempo hasta el evento (Celentano & Szklo, 2019, p. 362).
En la década del setenta, el estadístico británico David Cox desarrolló un método estadístico que permite analizar la relación entre variables predictoras y el tiempo hasta un evento, sin hacer suposiciones estrictas sobre la forma funcional de la distribución de supervivencia, lo que amplía significativamente la aplicabilidad del análisis de supervivencia (Boj del Val, 2017).
Más recientemente, esta técnica ha sido recuperada en diferentes ámbitos disciplinarios, como en la gestión bancaria, particularmente para la estimación de las probabilidades de incumplimiento de los deudores de créditos (Almeida, 2011; Ayala et al., 2007; Cáceres & Palacios, 2017; González & López, 2008; López, 2003; Obuda, 2014; Pérez-Duque, 2012). Sin embargo, su aplicación en ciencias sociales, especialmente en análisis sociológicos de procesos multivariantes autocorrelacionados, ha sido poco común.
Estos modelos probabilísticos han sido concebidos para comprender cómo diversos factores influyen en el tiempo que transcurre hasta que ocurre un evento específico, desplazando el enfoque del evento en sí al tiempo necesario para que tenga lugar. En el contexto de las trayectorias educativas, esta evaluación del tiempo es fundamental, ya que proporciona una comprensión más precisa del riesgo que los estudiantes enfrentan al comprometerse con sus estudios.
El análisis del tiempo hasta la ocurrencia de eventos clave, como la titulación o la desvinculación, es esencial para comprender las decisiones que los estudiantes toman a lo largo de su trayectoria educativa. La posibilidad de cuantificar cuánto tiempo se invierte o se retrasa un evento ofrece una perspectiva crítica para interpretar el impacto de diferentes factores en el éxito o el abandono académico. Esto convierte al análisis de supervivencia en una herramienta clave para entender y modelar las dinámicas de las trayectorias educativas.
Metodología
Descripción del instrumento
La estadística social ha adoptado diversas estrategias para modelar estas relaciones, desde análisis basados en regresiones lineales múltiples y logísticas hasta modelos jerárquicos lineales (o modelos de efectos mixtos), modelos de ecuaciones estructurales, análisis de trayectorias latentes y modelos de efectos mixtos generalizados, entre otras.
Estos modelos abarcan desde el análisis de datos longitudinales con múltiples factores hasta la modelización de transiciones discretas en el tiempo, como cambios en la salud o el empleo. Sin embargo, enfrentan desafíos cuando se trata de datos incompletos, tiempos de supervivencia desconocidos o variaciones en el tiempo de ocurrencia de eventos vitales.
En tales situaciones, los investigadores pueden recurrir a modelos específicos, como el análisis de supervivencia, diseñado para manejar datos temporales y eventos de duración, incluso aquellos censurados. Modelos como el de riesgos proporcionales de Cox permiten la modelación de riesgos con efectos variables en el tiempo y pueden adaptarse para considerar la autocorrelación temporal.
El análisis de supervivencia se centra en definir un período experimental y registra la información longitudinalmente, con registros del tipo "panel", lo que permite una vinculación directa entre los factores, el evento de interés y el paso del tiempo. Al enfocarse en el tiempo hasta el evento de interés, este análisis permite una modelación más específica y detallada de la duración observada, en lugar de simplemente predecir el resultado final. Adicionalmente, este enfoque permite analizar relaciones entre variables en un contexto en el que la manipulación directa no es posible, con datos recogidos retrospectivamente y con base en la observación de grupos naturales, lo que eleva la validez interna en diseños de tipo correlacional ex post facto, en los términos en que los describen Campbell y Stanley (1982). Estas son razones sobradas para su recomendación al momento de relevar, caracterizar y analizar las trayectorias estudiantiles.
Se aclaran algunos conceptos metodológicos clave. Se denomina sesgo por censura (o censura por derecha) a la pérdida de información por interrupción del vector antes de finalizado el período de observación o cuando la ventana de observación se cierra antes de ocurrido el evento. Esta dificultad es habitual cuando se observan grupos naturales. Por pérdida de casos o porque no resulta posible esperar a que acontezca el evento, algunos individuos no llegan a experimentar el evento estudiado.
Se denomina sesgo por truncamiento (o censura por izquierda) a aquel que se produce cuando el observable ingresa en la ventana de observación luego de haberse producido el evento que da inicio a la observación (no se observa la ocurrencia del evento origen) (Errandonea, 2022).
Como lo señala el propio Kaplan (Stalpers & Kaplan, 2018, como se cita en Errandonea, 2022):
En un estudio de supervivencia típico, la acumulación de un número suficiente de pacientes con una enfermedad específica suele tardar muchos años. (…) Estos pacientes, vivos o perdidos en el seguimiento, técnicamente se denominan observaciones “censuradas” o “incompletas”. Estas observaciones censuradas deben incluirse en la estimación de la tasa de supervivencia S(t). El problema de las observaciones incompletas en los estudios de supervivencia ya se había detectado en el siglo XIX (Hayward 1899a, b, 1900; Greenwood 1926).
Greenwood (1926) ya había señalado que si se eliminaban de la cohorte los pacientes vivos con una observación temporalmente más corta que la duración del estudio (es decir, “censurados” en el sentido gramatical y legal), entonces la estimación de supervivencia sería demasiado baja. Por otro lado, si se considera que los pacientes que vivieron durante un tiempo de observación más corto que la duración del estudio, se supone que permanecerán con vida hasta el final del estudio, la estimación de supervivencia terminaría siendo demasiado alta (pp. 213-214).
Desde esta perspectiva, se pueden tipificar cuatro tipos de observaciones: no truncada, no censurada; no truncada, censurada; truncada, no censurada; y truncada, censurada.
Adicionalmente, al analizar las trayectorias educativas, esta desagregación general puede aún resultar insuficiente. Por ejemplo, cuando es importante considerar diferencias en el tipo de censura por derecha (por abandono, cuando se niega el evento por interrupción de la participación experimental del sujeto, o por censura propiamente dicha, cuando se niega el evento por cierre de la ventana de observación).
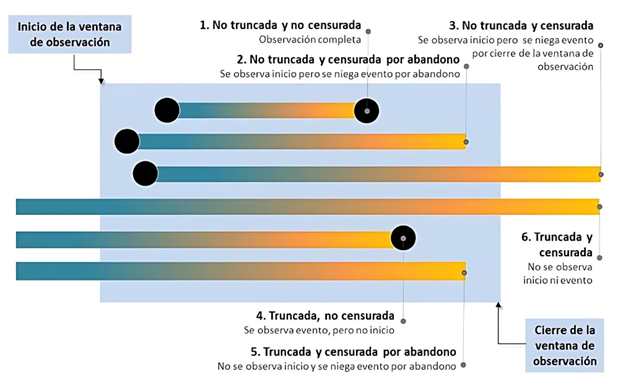
Ante estos desafíos analíticos, interesará ampliar la distinción anterior a seis tipos diferentes de observaciones (Figura 1):
- Observación completa. Se trata de trayectorias no truncadas y no censuradas con evento. La trayectoria comienza en el tiempo 0 o después y finaliza por observación del evento (información vectorial completa y se observa el evento).
- Se observa el inicio, pero se niega el evento por abandono. En este caso, la trayectoria no se ha visto truncada, pero sí censurada por cese de participación. La trayectoria comienza en el tiempo 0 o después y finaliza la participación en el experimento antes de que cierre la ventana de observación (información vectorial completa, pero se niega el evento por abandono).
- Se observa el inicio, pero se niega el evento por censura por derecha. Resulta cuando la trayectoria no se ha visto truncada, pero sí censurada por derecha. La trayectoria comienza en el tiempo 0 o después y finaliza la ventana de observación sin que se observe el evento (información vectorial completa, pero se niega el evento por el cierre de la ventana de observación).
- Se observa el evento, pero no el inicio por truncamiento. La trayectoria se ha visto truncada, pero no censurada con el evento. La trayectoria comienza con anterioridad al tiempo 0 y se registra el evento durante la ventana de observación (no se cuenta con información vectorial inicial, pero se observa el evento).
- No se observa el inicio por truncamiento y se niega el evento por abandono. Se trata de una trayectoria truncada y censurada por cese de participación. La trayectoria comienza con anterioridad al tiempo 0 y finaliza la participación en el experimento antes de que cierre la ventana de observación (no se cuenta con información vectorial inicial y se niega el evento por abandono).
- No se observa el inicio por truncamiento y se niega el evento por censura por derecha. La trayectoria se ha visto truncada y también censurada por derecha. La trayectoria comienza con anterioridad al tiempo 0 y finaliza la ventana de observación sin que se observe el evento (información vectorial incompleta, pero se niega el evento por el cierre de la ventana de observación).
- En varias situaciones de análisis correlacionales ex post facto en ciencias sociales, sobre todo las derivadas de la observación de grupos naturales, las observaciones pueden encontrarse, en el sentido antedicho, incompletas.
Una de las ventajas del análisis de supervivencia es que permite analizar los datos durante su desarrollo, es decir, no esperar en todos los casos al evento (Salazar Uribe et al., 2020, p. 11) y disponer para el análisis de los datos de técnicas paramétricas y no paramétricas.
Entre los procedimientos paramétricos más frecuentes se pueden señalar la distribución exponencial, la distribución de Weibull y la distribución Lognormal. Entre los procedimientos no paramétricos interesa destacar aquí el método de Kaplan-Meier y los procedimientos complementarios de Log Rank y la regresión de Cox (Arribalzaga, 2007; Rebasa, 2005).
Toda investigación requiere una cuidadosa elección de los métodos de análisis, con base en una adecuada evaluación de las características del objeto de estudio.
El efecto determinación social, en conjunto con la carencia de dimensiones medibles en escalas de intervalo o continuas, dan por tierra la pertinencia de sostener buena parte de los supuestos asumidos en muchas de las estrategias de análisis estadístico utilizadas.
No solo por las diferencias que específicamente demandan los objetos sociales en relación con otros objetos de conocimiento, sino porque provee instrumentos especialmente útiles en estos casos, nos concentraremos en las variantes no paramétricas del análisis de supervivencia, que lo tornan más adecuado cuando nos permite superar conjuntamente las dificultades señaladas y relativiza la validez interna de los resultados por medios alternativos.
Cuando el tiempo no es constante, la distribución es desconocida o compleja y es necesario considerar casos censurados, los modelos lineales generalizados enfrentan desafíos considerables. Estos desafíos se vuelven aún más difíciles cuando se necesita investigar grupos naturales de manera rastreable, lo que limita aún más los recursos estadísticos disponibles (Gómez & Cobo, 2004).
Entre los métodos no paramétricos más utilizados en el análisis de supervivencia se distinguen fundamentalmente dos (Gómez & Cobo, 2004, p. 51):
Aunque el método actuarial tiene sus aplicaciones específicas, el método de Kaplan-Meier generalmente se prefiere en situaciones en las que los datos de supervivencia son más complejos, censurados o irregulares, debido a su naturaleza no paramétrica y a su capacidad para manejar una variedad más amplia de escenarios (Arribalzaga, 2007).
Revisemos muy brevemente sus diferencias más importantes. El método actuarial utiliza tasas de supervivencia, lo que representan la probabilidad de que una persona de una determinada edad sobreviva durante un período específico. Estas tasas se derivan de las tablas de mortalidad y se utilizan para calcular las probabilidades acumulativas de supervivencia. Las tablas de mortalidad, que son registros históricos de las tasas de mortalidad observadas en una población específica a lo largo del tiempo, proporcionan la base para calcular las probabilidades de supervivencia en diferentes edades (Arribalzaga, 2007).
Es comúnmente utilizado en industrias como seguros y pensiones e implica dos premisas para el tratamiento de los datos (Fernández, 1995):
- Todos los eventos ocurren aleatoriamente durante un intervalo dado. Esto puede suponer un sesgo importante cuando los intervalos son grandes, cuando hay numerosos eventos o cuando los eventos no ocurren a mitad de los intervalos. Dado que las tablas de mortalidad generalmente se presentan en intervalos de edad discretos, el método actuarial utiliza técnicas de interpolación y extrapolación para estimar las tasas de supervivencia para edades específicas que pueden no estar incluidas en las tablas. Esto limita su flexibilidad cuando se trata de datos que no se ajustan a esas tablas. Esto puede resultar en estimaciones menos precisas cuando los datos no cumplen estrictamente con esos supuestos.
- La probabilidad de la supervivencia en un período de tiempo es independiente de la probabilidad de supervivencia en los demás períodos. En tal caso, el análisis puede verse sesgado ante casos censurados, ya que no maneja bien la censura, en comparación con el método de Kaplan-Meier, diseñado específicamente para lidiar con observaciones censuradas de manera más robusta.
Ha sido concebido para estimar la función de supervivencia a partir de datos censurados, los que resultan comunes en estudios de supervivencia (Lifshitz, 2014, p. 163), en la medida en que, como se dijo, algunos sujetos no experimentan el evento de interés durante el período de observación (Arribalzaga, 2007; Fernández, 1995).
Esta técnica genera una curva de supervivencia que muestra la proporción de sujetos que sobreviven hasta un tiempo específico. La curva se construye a medida que ocurren eventos o censuras en el conjunto de datos, se basa en la estimación de las probabilidades condicionales en cada punto temporal cuando tiene lugar un evento o una censura y toma el límite del producto de esas probabilidades para estimar la tasa de supervivencia en cada punto temporal.
No hace tantas suposiciones sobre la distribución subyacente de los tiempos de supervivencia como el método actuarial, lo que lo hace más adecuado cuando la forma de la distribución no es conocida o puede ser compleja (Gómez & Cobo, 2004): es más flexible en términos de intervalos de tiempo (efectivo con intervalos desiguales y no requiere que todos los eventos sean registrados en momentos iguales) y es particularmente útil para comparar las tasas de supervivencia entre diferentes grupos o tratamientos. Por ello, es robusto y más preciso en la estimación, especialmente en presencia de datos censurados, en situaciones más realistas y complejas.
Es necesario señalar también que, como el objeto de análisis no es el evento, sino el tiempo transcurrido al evento, no distingue entre diferentes tipos de evento y, por lo tanto, para comparar el tiempo involucrado en eventos diferentes o diferenciar formatos de censura de los eventos necesita ser rotado y/o redefinido el evento de interés.
En su famoso artículo “Nonparametric Estimation from Incomplete Observations”, Kaplan y Meier (1958) señalaban que, “a pesar de la incompletitud resultante de los datos, se desea estimar la proporción P(t) de elementos en la población cuyas vidas útiles excederían t (en ausencia de tales pérdidas), sin hacer ninguna suposición sobre la forma de la función P(t)” (p. 457).
Sin embargo, este procedimiento aplicado a cada tramo (intervalo entre dos eventos) no tiene en cuenta los casos perdidos anteriormente. Si no hay pérdidas, todo se cancela excepto el primer denominador N y el último numerador n(t), y p(t) se reduce a la estimación binomial usual formalizada por la ley de Laplace (casos probables/casos posibles): ch1
De manera que P(t) es una función escalonada que cambia su valor solo en las edades observadas de muerte, en las que es discontinua: ch2
De esta forma se propone estimar puntualmente la supervivencia acumulada como una función condicional de la probabilidad de supervivencia previa: ch3
Para la estimación de los límites del intervalo de confianza (IC), se usa una aproximación a la función normal, con la fórmula de estimación del error estándar de Greenwood: ch4
De manera que, por ejemplo, con una precisión del 95 % el intervalo de confianza se puede calcular de la siguiente manera: ch5
Con el objetivo de proporcionar una idea de la velocidad con que se observa cada nuevo evento (“velocidad de fallecimiento”), se calcula la “tasa de mortalidad instantánea”, “función de fallo”, “función de riesgo” o, genéricamente, función de impacto.
De forma alternativa a la supervivencia, la función de impacto (h(t)) estima la probabilidad de que en dicho tiempo se observe un evento: ch6
En palabras de Kaplan y Meier (1958), se propone un cálculo de la probabilidad tramo a tramo:
Para muestras aleatorias de tamaño N, la estimación del producto-límite (PL) se puede definir de la siguiente manera: Enumere y etiquete las N vidas útiles observadas (ya sea hasta la muerte o la pérdida) en orden de magnitud creciente, de modo que se tenga o < t₁ < t₂ < ... < tn. Luego, P(t) = Π ((N - r) / (N - r + 1)) , donde r asume aquellos valores para los cuales tᵣ < t y para los cuales tᵣ mide el tiempo hasta la muerte. Esta estimación es la distribución, sin restricciones en cuanto a forma, que maximiza la verosimilitud de las observaciones. Otras estimaciones que se discuten son las actuariales (que también son productos, pero con el número de factores generalmente reducido por agrupamiento); y las estimaciones de muestra reducida (RS), que requieren que las pérdidas no sean accidentales, de modo que los límites de observación (tiempos potenciales de pérdida) sean conocidos incluso para aquellos elementos cuyas muertes son observadas. Cuando no ocurren pérdidas a edades menores que t, la estimación de P(t) en todos los casos se reduce a la estimación binomial usual, es decir, la proporción observada de sobrevivientes (p. 457).
En el método actuarial se introducen intervalos de tiempo constantes, previamente definidos por el investigador, y la forma de cálculo sería la siguiente: ch7
Sin embargo, luego de haber ordenado crecientemente los tiempos a que se producen los eventos, el método de Kaplan-Meier permite calcular la función de impacto de la siguiente manera (Rodríguez Barranco, 2017, p. 10): ch8
Así, este instrumento se torna especialmente apropiado cuando el evento ocurre en lapsos no previstos por las tablas de mortalidad originales o no regulares en el tiempo. Es capaz de asumir no solo períodos de diferente duración, sino períodos tan cortos como los propios de acaecimiento de cada evento. Adicionalmente, el instrumento de interpretación se torna bastante más apropiado cuando el evento se ha considerado deseable: “positivo”.
Por ello, la función de impacto se estima como la probabilidad de que en dicho tiempo se observe un evento (hasta un límite infinitesimal, mediante el método del límite de producto de Kaplan-Meier) (Arribalzaga, 2007): ch9
Adicionalmente, por intermedio de la regresión de Cox, el modelo permite introducir la noción de “tiempo no constante”, en relación con su interacción con terceras variables de interés. Esta variabilidad, como se dijo, puede no contemplar otros modelos de estimación probabilística habituales.
Por ejemplo, en comparación con la regresión logística, que se utiliza para modelar la probabilidad de que ocurra un evento con datos categóricos binarios, en el que el resultado es "éxito" o "fracaso", como la presencia o ausencia de una enfermedad, en función de uno o más predictores, la aplicación del método de Kaplan-Meier complementariamente permite estimar la función de supervivencia, como el tiempo de supervivencia hasta un evento.
En tanto el método de Kaplan-Meier no hace suposiciones sobre la distribución de los tiempos de supervivencia, las regresiones logísticas suponen una relación logarítmica lineal entre los predictores y la probabilidad del evento. Produce una curva de supervivencia que muestra la probabilidad acumulativa de supervivencia a lo largo del tiempo. Las regresiones logísticas proporcionan coeficientes que indican el cambio en la probabilidad logarítmica del evento para un cambio unitario en el predictor con independencia del tiempo transcurrido.
Como se dijo, el método de Kaplan-Meier puede manejar datos cuando la información sobre el tiempo de supervivencia no está disponible para todos los sujetos (censurados). Mientras que las regresiones logísticas, no manejan naturalmente la censura y en general requieren datos completos.
Si bien las regresiones logísticas permiten naturalmente la inclusión de covariables para ajustar el modelo a otras características relevantes, el método de Kaplan-Meier puede complementarse con la regresión de Cox para incorporar indirectamente covariables en el modelo y superar esta desventaja relativa.
Por lo dicho, el análisis de supervivencia, clásicamente concebido como un procedimiento para estimar el tiempo probable de ocurrencia de un evento específico con base en tratamientos bivariados comparados, requiere la incorporación de instrumentos que faciliten análisis más complejos y puedan evaluar comparadamente los niveles de más de dos efectos y su significación en múltiples tratamientos.
En este sentido, existen varios instrumentos adecuados para la sofisticación y la validación de los modelos. Por ejemplo:
- La ya señalada regresión de Cox, que eleva el análisis al nivel multivariado, mediante la incorporación de covariables.
- El método de log-rank, que permite determinar si hay diferencias significativas en las tasas de supervivencia entre los grupos comparados.
- La posibilidad de incorporar rotaciones en la definición del evento, al realizar sendas reiteraciones de los procesamientos de análisis mediante los recursos provistos por la regresión de Cox.
Al asumir que la censura no es informativa, los tiempos de evento y de censura son considerados independientes: cada participante i puede presentar un tiempo al evento Ti (observación no censurada: en este caso, sabemos que el tiempo de censura hubiera ocurrido después de t = T¡) o un tiempo a la censura C¡ (observación censurada: en este caso, sabemos que el evento hubiera ocurrido después de t = C¡), aunque solo uno de los dos es observable.
En consecuencia, la relación entre nk y nk+1 (intervalos consecutivos en la variable tiempo) depende de la cantidad de eventos y de censuras (Ducrocq & Gómez, 2000, p. 238-239): ch10
Como la función de impacto se define como la tasa instantánea de falla en el tiempo t, su fórmula básica es: ch11
Examinemos el procedimiento con base en un ejemplo.
Se estimó la probabilidad de la obtención de un título universitario entre los estudiantes que ingresaron en 2010 a la Universidad de la República (Udelar), en un período determinado, utilizando datos censurados. Además, se analizaron los efectos de varios atributos de los estudiantes para relacionar la evolución individual de los participantes y la forma en que influyeron dichos factores en las transiciones académicas observadas.
Luego de estimar la probabilidad de obtener el título en un determinado tiempo (p(t)) y el riesgo instantáneo o función de impacto de no obtenerlo (h(t)), para estudiantes provenientes de hogares universitarios (u) y estudiantes provenientes de hogares no universitarios (nu) de manera independiente, se evaluaron las probabilidades condicionales relativas de ambos grupos.
Habiéndose obtenido una p(t nu )=0,886, con un h(t nu )=0,005, en estudiantes provenientes de hogares no universitarios y p(t u )=0,820, con un h(t u )=0,006, en estudiantes provenientes de hogares universitarios, para un estrato de t específico, el valor de comparación se halla mediante la comparación de las respectivas tasas de cambio (h(t)/ p(t)), de la siguiente manera: ch12
A partir del ejemplo, se puede observar que la tasa de cambio en la función de supervivencia en el tiempo es ligeramente mayor para los primeros en comparación con los segundos, en el mismo punto en el tiempo.
Como el valor de t generalmente se considera un cambio infinitesimal en el tiempo y se mantiene constante para todos los estratos, esta forma de estimación es independiente del tamaño o duración del estrato al que se aplique la derivada.
Para evaluar la influencia de múltiples variables predictoras (covariables) en la función de impacto de un evento a lo largo del tiempo (h(t)), se utiliza la regresión diseñada a tal fin por Cox en 1970.
Este recurso permite investigar la relación entre las variables predictoras y la función de impacto (h(t)), para la realización de los análisis multivariables necesarios para controlar y evaluar el impacto de múltiples factores al mismo tiempo.
De manera que, mediante la regresión de Cox, se estima el riesgo relativo (cociente de riesgos instantáneos) asociado con cada covariable, lo que permite cuantificar cómo las variables afectan la función de impacto a lo largo del tiempo.
Cuando estamos analizando datos, es importante asegurarnos de que las diferencias que encontramos entre grupos sean significativas y no solo aleatorias. Para hacer esto necesitamos una manera de medir cuán válidas son esas diferencias. Podemos usar algo llamado pruebas de rango logarítmico, que básicamente son métodos para comparar las tendencias entre diferentes grupos. En lugar de simplemente confiar en nuestros ojos para ver si hay diferencias, estas pruebas nos ayudan a cuantificar y verificar si realmente hay perfiles distintos entre los grupos que estamos estudiando. Es como usar una lupa para examinar las diferencias y estar seguros de que son reales y no solo una casualidad.
La prueba de log-rank es una herramienta estadística muy utilizada para comparar las tasas de eventos entre dos o más grupos a lo largo del tiempo. Compara los registros observados con las observaciones esperadas bajo la hipótesis nula de que no hay diferencias en las tasas de supervivencia entre los grupos. Y, por lo tanto, es útil para determinar si hay diferencias significativas entre las tasas de supervivencia de diferentes grupos.
Ilustración del uso de la metodología mediante un ejemplo concreto
En el apartado anterior se estableció que la conjunción de las dimensiones que caracterizan a ciertos objetos, como ocurre al estudiar trayectorias estudiantiles, los hacen difíciles de tratar por algunos de los procedimientos clásicamente adoptados en las ciencias sociales.
En este sentido, Beltrán Villalva (1985) sugiere que el método científico debe adecuarse rigurosamente al objeto de estudio, caracterizando así a la sociología como una disciplina única que no encaja completamente ni en las "ciencias del espíritu" ni en las ciencias físico-naturales:
La propuesta, pues, aquí formulada es la adecuación del método a la dimensión considerada en el objeto, y ello no de manera arbitraria e intercambiable, sino con el rigor que el propio objeto demanda para que su tratamiento pueda calificarse de científico. (…) De aquí la peculiaridad de la sociología, que no se constituye como una de las viejas 'ciencias del espíritu’ porque no trata solo de cuestiones espirituales (valga la forma de llamarlas), pero tampoco como ciencia físico-natural, ya que su objeto se niega a dejarse encasillar en tal categoría (p. 39).
Allison (2010) destacaba en particular algunos desafíos al momento de analizar datos con características comunes que son difíciles de manejar con métodos estadísticos convencionales: la censura y las covariables dependientes del tiempo. El seguimiento de individuos con el objetivo de determinar cómo la ocurrencia y el momento de la ocurrencia de ciertos eventos dependen de varias covariables es un enfoque central en la investigación sociológica. Algunas de estas covariables, como la raza y la edad, permanecen constantes durante el intervalo de un año. Otras, como el estado civil y laboral, podrían cambiar en cualquier momento durante el período de seguimiento.
Una posibilidad es realizar un análisis de regresión logística con una variable dependiente dicotómica. Sin embargo, este análisis ignora la información sobre el momento del evento. Al menos, ignorar esa información debería reducir la precisión de las estimaciones.
Una solución a este problema es hacer que la variable dependiente sea el período de tiempo entre la liberación y el primer arresto y luego estimar un modelo de regresión lineal convencional. Pero ¿qué se hace con las personas que no registraron el evento durante el año de seguimiento? Estos casos se denominan censurados. Hay un par de métodos ad hoc obvios para tratar casos censurados, pero ninguno funciona bien. Un método es descartar los casos censurados. Ese método podría funcionar razonablemente bien si la proporción de casos censurados es pequeña. Sin embargo, si son muchos datos que descartar, se ha demostrado que pueden producirse grandes sesgos. Alternativamente, se podría fijar el tiempo del evento en un año para todos aquellos que no lo registraron. Sin embargo, esto es claramente una subestimación, y es posible que algunos de esos nunca registren el evento. Nuevamente, pueden ocurrir grandes sesgos (Allison, 2010, p. 4).
El estudio de las trayectorias educativas en la educación superior presenta las dificultades señaladas. En este contexto, el análisis de supervivencia mediante el método de Kaplan-Meier es preferible, ya que evita hacer suposiciones fuertes sobre la distribución de los tiempos hasta el evento. Además, este método es especialmente útil cuando los eventos son proporcionalmente raros. Las contribuciones de la regresión de Cox y el método Long-Rank para validar la significación de las diferencias fortalecen aún más esta preferencia.
En el estudio de la cohorte de ingreso en 2010 a carreras de grado de la Udelar, los investigadores de la Unidad de Sistemas de Información de la Enseñanza (Usien) de la Comisión Sectorial de Enseñanza optaron por un diseño cuasiexperimental de tipo correlacional ex post facto, siguiendo las directrices establecidas por Campbell y Stanley (1982) (Errandonea, 2023a). Este enfoque permitió analizar relaciones entre covariables en un contexto en el que la manipulación directa no era posible y los datos fueron recogidos retrospectivamente con base en la observación de grupos naturales. Esta estrategia supuso el estudio de la evolución individual de los participantes a lo largo del tiempo, modelando cómo influyeron diferentes factores en las transiciones de interés.
Revisemos algunos hallazgos de esta experiencia para ejemplificar la utilidad del instrumento.
El estudio de la Usien analiza las actividades académicas de los estudiantes de carreras de hasta cinco años de duración teórica, durante un período de observación de ocho años lectivos (2010 a 2017).
Se trató de la observación de un grupo natural que incluía una importante proporción de unidades de observación que no alcanzaron a registrar el evento, dado que se interrumpió el vector por censura por derecha (se niega el evento por cierre de la ventana de observación) o, de manera anticipada, por “abandono” o “desvinculación” (se niega el evento por “mortalidad muestral”). En consecuencia, la exploración preliminar se concretó mediante un análisis de supervivencia con base en el método de Kaplan-Meier. Para la incorporación al análisis de covariables, se procedió mediante la regresión de Cox. Y, para la valoración de la significación de las diferencias observadas entre los grupos, se recurrió al método de log-rank.
El estudio se sustanció en los registros de las instancias académicas de 9.562 estudiantes inscriptos en 2010 en la Udelar en carreras de grado (de hasta 5,5 años de duración teórica). Solo se utilizaron los registros correspondientes a estudiantes de hasta 30 años de edad al momento de su inscripción. La estrategia consistió en analizar las trayectorias de los estudiantes en procura de la obtención de un primer título universitario (evento de observación).
Adicionalmente, se valoró el grado en que diferentes atributos individuales podían resultar asociados al tiempo invertido por los estudiantes en la obtención del título, particularmente, la estimación del tiempo transcurrido hasta el acaecimiento del evento de graduación o, en su defecto, del evento de “interrupción definitiva de las actividades académicas” (desvinculación).
Cuando el último registro se correspondió con la titulación, se la consideró una observación completa (con presencia del evento). Cuando no se correspondió con la graduación, fue conceptualizada como una observación incompleta. El estudio consideró las observaciones incompletas como censuradas en las dos modalidades señaladas: por abandono, si se registró antes del año de cierre de la ventana de observación (2017); o, si ocurrió por el cierre de la ventana de observación (2017), como censura por derecha.
Resultados
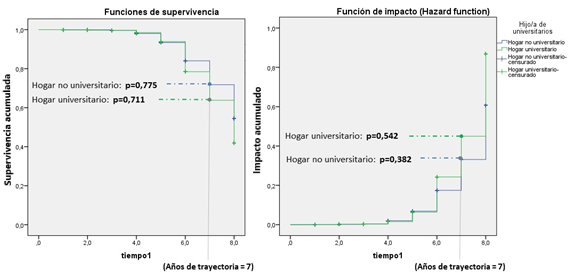
La Figura 2 permite la interpretación de algunas de las curvas de supervivencia e impacto observadas en el estudio.
Una función de supervivencia de p=0,775 y una función de impacto de p=0,382 al séptimo año de cursado entre los estudiantes provenientes de hogares no universitarios significa que la probabilidad de que un estudiante proveniente de un hogar no universitario no obtenga el título habilitante antes de los siete años es del 77,5 % y la probabilidad de que al menos un estudiante lo obtenga en idéntico período es del 38,2 %.
Complementariamente, el hecho de que la función de supervivencia para los estudiantes provenientes de hogares universitarios al séptimo año de cursado fuera p=0,711 y la función de impacto de p=0,542 significa que la probabilidad de que un estudiante proveniente de un hogar universitario no obtenga el título habilitante antes de los siete años es del 71,1 % y que la probabilidad de que al menos un estudiante obtenga el título habilitante dentro de los primeros siete años es del 52,4 % (Figura 2).
Con base en los valores de significación obtenidos (Tabla 1), para las variables sexo al nacer (Sexo_cod), duración teórica de la carrera (Dur_teo_carr) y máximo nivel educativo alcanzado en el hogar del estudiante (hogar_univ), existe suficiente evidencia para rechazar la hipótesis nula de que los coeficientes no difieren significativamente de cero. Sin embargo, esto no se observó en el caso de la variable tipo de carrera (Tipo_carr), cuyo valor p (Sig.=0,166) no es menor a 0,05.
Tabla 1: Coeficientes de las variables en la ecuación en el análisis de estimaciones de máxima verosimilitud del modelo en covariables
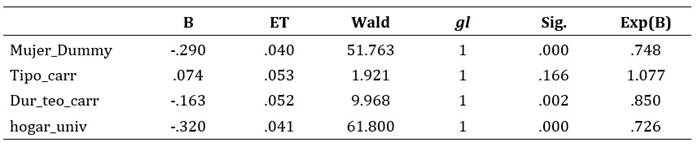
Nota: Procesamiento propio con base en datos de la Udelar anonimizados (2010-2017), proporcionados por la Usien, provenientes de consultas prediseñadas a la plataforma Trébol (SGAE, Seciu, Udelar).
Las razones de peligro instantáneo (Exp(b)) indican que el riesgo relativo es significativamente diferente de 1 en dos de las variables señaladas (Mujer_Dummy y hogar_univ), y una tercera (Dur_teo_carr) también muestra significancia estadística. Por ejemplo: Exp(B)=0,726 para hogar_univ sugiere que, ante un cambio unitario en la variable predictora (1=Hogar universitario), la probabilidad de titulación disminuye en un 27,4 % (en relación con 0=Hogar no universitario). A partir del valor de Exp(B) para Tipo_carr (1,077), por no ser estadísticamente significativo (p=0,166), no permite concluir que el tipo de carrera tenga un efecto claro sobre la titulación.
Complementariamente, la variable hogar_univ muestra una variación significativa entre los patrones (Tabla 2): entre los estudiantes que tienen al menos un universitario en su hogar y aquellos que no tienen universitarios en su hogar.
Tabla 2: Medias de las covariables y valores de los patrones
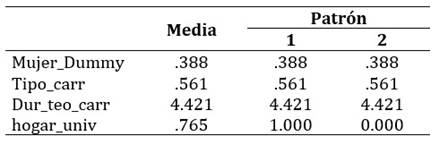
Nota: Procesamiento propio con base en datos de la Udelar anonimizados (2010-2017), proporcionados por la Usien, provenientes de consultas prediseñadas a la plataforma Trébol (SGAE, Seciu, Udelar).
A partir de la información anterior, se examinaron los efectos de estas covariables y de los factores combinados entre sexo y edad, en el marco de una parcialización del análisis de regresión con base en el máximo nivel educativo alcanzado en los hogares de procedencia de los estudiantes.
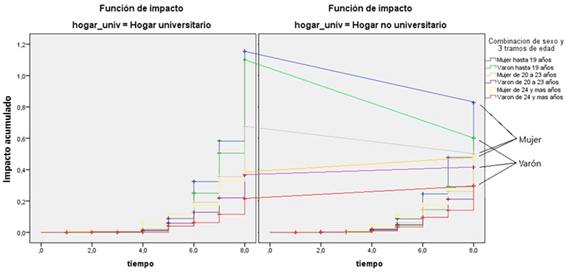
Como se observa en la Figura 3, las mujeres tienen una probabilidad significativamente mayor de graduarse en comparación con los hombres. Este hallazgo sugiere una ventaja académica femenina en este grupo específico de estudiantes, con relativa independencia del nivel educativo del hogar de procedencia.
Sin embargo, lo más relevante resulta de analizar, en el marco de la segmentación por nivel educativo del hogar, la manera en que la interacción entre edad y sexo tiende a especificar las probabilidades parciales de graduación:
- Mujeres jóvenes (menores de 19 años) tienen la mayor probabilidad de graduarse.
- Hombres y mujeres de 20-23 años también muestran una mayor probabilidad de graduarse, pero las mujeres en este grupo tienen un menor aumento en la probabilidad comparado con los hombres.
- Hombres mayores (24 años o más) no muestran un aumento significativo en la probabilidad de graduación.
- Mujeres mayores (24 años o más) siguen mostrando una probabilidad significativamente mayor de graduarse.
Discusión
La información obtenida es en sí importante, pero adquiere sentido indicativo en relación con las acciones en materia de política educativa venideras, cuando se especifican dichas probabilidades en el marco de covariables de interés.
Como se dijo, el método de Kaplan-Meier interpone recursos analíticos sobre relaciones bivariadas. Para poder considerar la influencia de terceros factores, el referido estudio procedió a complementar el análisis corriendo una regresión de Cox.
En el ejemplo la dirección y magnitud de la relación entre algunas variables predictoras y la función de impacto (hazard) de efectivamente lograr la titulación (evento de interés) sugieren una asociación inversa.
La variabilidad señalada de la variable hogar_univ (Tabla 2) podría ser relevante para entender las diferencias en la probabilidad de titulación, dado que en el análisis previo se encontró que esta variable era significativa.
El análisis de la cohorte de 2010 de la Udelar, basado en el modelo de regresión de Cox, revela diferencias significativas en la probabilidad de graduación entre los estudiantes cuyos padres poseen títulos universitarios y aquellos cuyos padres no los poseen.
Al examinar los efectos de los factores combinados entre sexo y edad, en el marco de una parcialización del análisis de regresión con base en el máximo nivel educativo alcanzado en los hogares de procedencia de los estudiantes, también se observan diferencias condicionales de probabilidad de graduación que resultan de interés.
La nueva información confirma que los hijos de universitarios y las mujeres tienen una probabilidad significativamente mayor de graduarse en comparación con los hombres y con los hijos de hogares no universitarios. Este hallazgo sugiere una ventaja académica femenina, que se especifica incrementando las diferencias de probabilidad de graduarse por sexo y edad, en el grupo específico de quienes son primera generación de universitarios. Se confirma la importante influencia del nivel educativo del hogar de origen y de la interacción de sexo y edad para entender las diferencias en las tasas de graduación entre los estudiantes de la cohorte de 2010 de ingreso a carreras de grado de la Udelar:
- A partir de los cinco años de estudio, que es el tiempo teórico promedio para terminar una carrera, empiezan a hacerse evidentes diferencias significativas en las probabilidades de graduación entre los distintos grupos. Estas diferencias se hacen aún más pronunciadas a medida que se analizan trayectorias de mayor duración.
- Existe una posible relación entre la probabilidad de completar una carrera universitaria y el nivel educativo de los padres. En particular, las mujeres tienen una mayor probabilidad de graduarse, especialmente las más jóvenes, menores de 19 años. Esta ventaja también se observa entre los estudiantes de 20 a 23 años cuando sus padres tienen títulos universitarios.
- En los casos en los que los padres no han terminado la universidad, las mujeres siguen mostrando una mayor probabilidad de graduarse. Sin embargo, los varones menores de 19 años tienen una menor probabilidad de graduarse en comparación con sus compañeras de la misma edad.
- La probabilidad de graduación varía según la edad, el género y el nivel educativo del hogar. Sin embargo, entre los estudiantes mayores de 24 años y los varones de entre 20 y 23 años, aquellos provenientes de hogares con un nivel educativo más bajo muestran una mayor probabilidad de graduarse.
La validación de los resultados mediante la comparación robusta entre diferentes grupos y tratamientos enfatiza la capacidad para revelar diferencias significativas en las trayectorias estudiantiles. Estos factores son clave para entender cómo y por qué los estudiantes permanecen o abandonan la educación superior. Esto se vincula con el diseño de políticas acertadas para mejorar la retención estudiantil y proporciona una base para interpretar los resultados del análisis de supervivencia y la comprensión más profunda de cómo los estudiantes evalúan el riesgo y las recompensas asociadas con la continuación de sus estudios.
La relevancia del tipo de análisis de datos se subraya al integrar factores como el origen de clase y la toma de decisiones racional basada en la evaluación de costos y beneficios, tal como sugieren los trabajos de Boudon (Errandonea, 2022).
Conclusión
Por lo expuesto, el análisis de supervivencia, especialmente utilizando el método de Kaplan-Meier y la regresión de Cox, representa un enfoque metodológico que se justifica, en función de su capacidad de aportar al debate actual, con información complementaria sobre los factores institucionales, sociales, socioeconómicos y culturales que influyen en la permanencia y la desvinculación de los estudiantes.
La validación de los resultados mediante la comparación robusta entre diferentes grupos y tratamientos enfatiza la capacidad para revelar diferencias significativas en las trayectorias estudiantiles. Estos factores son clave para entender cómo y por qué los estudiantes permanecen o abandonan la educación superior. Esto se vincula con el diseño de políticas acertadas para mejorar la retención estudiantil y proporciona una base para interpretar los resultados del análisis de supervivencia y la comprensión más profunda de cómo los estudiantes evalúan el riesgo y las recompensas asociadas con la continuación de sus estudios.
En conclusión, destacar la importancia y la utilidad del análisis de supervivencia para la investigación educativa en las condiciones señaladas ha sido el objetivo principal del presente artículo. A través del estudio de las trayectorias académicas en la Udelar, se ha demostrado cómo esta metodología, en particular el método de Kaplan-Meier, es especialmente efectiva para manejar datos censurados y complejos y cómo, complementada con la regresión de Cox y el método de log-rank, fortalece la validación de resultados.
Las conclusiones aportan al objetivo del artículo al destacar cómo el análisis de supervivencia permite identificar diferencias significativas en los tiempos y la velocidad de graduación entre distintos grupos de estudiantes. Estas diferencias, que se acentúan a medida que las trayectorias se extienden más allá del tiempo teórico promedio, demuestran la capacidad del análisis de supervivencia para captar la influencia de factores como el género, la edad y el nivel educativo del hogar, no solo en la probabilidad de graduación, sino también en la inversión de tiempo que fuera requerida. Constituye una herramienta robusta para estudiar trayectorias estudiantiles de manera más precisa.