Introducción
En los tiempos que van, se sigue espectando bajas performances de nuestros estudiantes de Educación Básica, en el área de Matemática. En las pruebas de alcance internacional, nacional y regional, los resultados indican que el desempeño del mayor porcentaje de estudiantes se etiqueta con el Nivel 1 o debajo del Nivel 1, lo que significa que el nivel de logro alcanzado por nuestros estudiantes, en el área curricular de matemática, les permite resolver solamente los problemas simples, ejercicios que solamente requieren ejecutar rutinas o realizar operaciones básicas (Ministerio de Educación del Perú, 2018). Esta situación preocupa a las autoridades educativas, a los docentes, a los padres de familia y también a los estudiantes.
Los países de América del sur, principalmente, se ubican en los últimos lugares, con puntajes menores al promedio de la OECD. Hay algunos que están mejor que otros y también se evidencia que los estudiantes de algunos países van incrementando sus promedios entre prueba y prueba, sin embargo, esas cifras y logros se movilizan en el espacio de los que están mal y no salen, ni hay perspectivas de salir en el corto plazo, de ese escenario (Fernanda, 2019; OECD, 2023).
Esta situación descrita en cada uno de los países, después de la publicación de resultados, genera malestar en la población y también apresura la toma de decisiones en la alta dirección educativa de cada país. Así por ejemplo se hicieron modificaciones curriculares con matices muy finos para particularizar cada sistema educativo (Montes & Rivas, 2015). El enfoque por competencias en todas las áreas curriculares y el enfoque de la resolución de problemas en el área de Matemática se viene ejecutando en países como Chile, Colombia, Ecuador, Uruguay y Perú, entre otros (Ministerio de Educación de la Nación Argentina, 2019; Ministerio de Educación Nacional de Colombia, 2006; Ministerio de Educación del gobierno de Chile, 2018; Ministerio de Educación del Perú, 2016). Claro que el enfoque por competencias hoy en día no es una innovación porque este se abrió camino, con mucha intensidad, en la primera década de este siglo y el enfoque de resolución de problemas, en el área de Matemática, tiene sus inicios en la segunda década del siglo pasado con Brouwer (Resnick & Ford, 1998), impulsado por Pólya a la mitad del siglo (Pólya, 1969) y concretizado en los primeros años de este siglo con los resultados de las primeras pruebas PISA (OCDE, 2017).
En países como el nuestro, se han desarrollado programas de capacitación, entrenamiento o fortalecimiento de las capacidades docentes, en los que a pesar de las críticas por las formas y por el contenido de estas, han servido a una proporción, todavía muy pequeña, de cuando menos hacer reflexionar sobre la didáctica de la matemática y también para orientar técnicamente el desempeño profesional de los docentes, para lograr desarrollar en sus estudiantes las competencias del área de Matemática.
Desde otra arista, se afronta el problema a través de las investigaciones. Los resultados de las investigaciones que abordan la problemática del rendimiento bajo en el área de Matemática tratan, por ejemplo, sobre la aplicación de diversas estrategias, en entornos virtuales y presenciales, con materiales lúdicos, manipulables o de participación en equipo, para desarrollar competencias y para el aprendizaje de contenidos temáticos de matemática. Estas investigaciones y su data obran en los repositorios de las universidades y en las principales bases de datos académicas. En todas, se muestran los aportes que puntualmente permiten una mejor comprensión de lo principal del área de Matemática y también procedimientos y experimentos para que los docentes lo repliquen, en aras de mejorar los procesos de enseñanza y aprendizaje.
Para superar en parte el reto de contribuir a superar el bajo nivel de logro de las competencias del área curricular de matemáticas, proponemos diseños de sesiones de aprendizaje, para que los docentes puedan contextualizarlos y utilizarlos con sus estudiantes. Se realizó la investigación para mejorar la calidad del aprendizaje de los estudiantes del primer año de secundaria, utilizando la estrategia de Pólya adicionándole un pasatiempo tradicional de los niños y jóvenes: completar un álbum. Trabajar didácticamente con el álbum, motivar a los estudiantes y mejorar el desarrollo de la competencia de resolución de problemas de dominios aritméticos y algebraicos, relacionados con las operaciones aritméticas básicas y el planteo de ecuaciones, que son propósitos relativamente complicados para lograr en estudiantes que recién terminan primaria.
Sin ser la solución a los problemas descritos, es una alternativa que contribuye puntualmente. El uso del recurso didáctico Álbum-Mátic (A-M), en el desarrollo de la estrategia de Pólya, motiva y permite desarrollar las competencias de resolución de problemas de cantidad y, regularidad, equivalencia y cambio (Minedu, 2016); que son dos de las competencias del área curricular de matemática que se propone en el Currículo Nacional de Educación Básica (CNEB).
El A-M como todos los álbumes es una publicación que viene con espacios vacíos y numerados en los que deben ser pegados los cromos, en este caso de fotos representativas de las actividades culturales y económicas de la provincia y de las estudiantes de la muestra de estudio.
Se plantearon problemas sobre situaciones del entorno económico, social y cultural de la provincia. Las estudiantes del primero de secundaria individualmente y en grupo resolvían los problemas utilizando algunas técnicas matemáticas, en relación con la naturaleza de los problemas. Como premio a su desempeño conseguían las fotografías para colocarlas en su A-M.
El estudio refiere el uso del A-M en el desarrollo de la estrategia de Pólya, para la resolución de problemas matemáticos, con el sustento teórico de los recursos didácticos y lo que difunden los estudios empíricos sobre la estrategia de Pólya y la resolución de problemas, de diferentes investigadores, quienes en diferentes niveles educativos comprobaron los beneficios de la estrategia Pólya en el desarrollo de la competencia de resolución de problemas (Morales, 2021; Oliveros et al., 2021; Sánchez & Valencia, 2021).
La estrategia de Pólya en la resolución de problemas
Así como Fripp (2012) se preguntó sobre cómo enseñar la geometría en distintos contextos, es válido reflexionar sobre ¿cómo se media el desarrollo de la competencia: resuelve problemas de cantidad, en distintos contextos?, ¿qué procesos se debe considerar al planificar una sesión?, ¿habrá diferencias con la planificación de desarrollar otras habilidades u otras áreas curriculares? La respuesta tiene que ver con la metodología que se impregna en los diseños de sesiones de aprendizaje. Para Jaramillo (2008) citado por Fripp (2012, p. 56) tiene que ver con construcciones metodológicas, que son “las maneras específicas o los estilos particulares construidos por los docentes en sus prácticas de enseñanza, para propiciar la adquisición de conocimiento y los procesos de formación de los estudiantes”.
En esas maneras específicas de aprender a resolver problemas, de desarrollo de competencias en el área de Matemática se inscribe la estrategia de Pólya con el uso del Álbum-Mátic, que facilita la resolución con técnicas que basan su eficacia en la activación de los procesos mentales y la generación de compromisos en los estudiantes, implicando en este proceso, sus emociones y afectos, así como el desarrollo de estrategias de resolución de problemas matemáticos, lo que equivale a decir que deriva en una estrategia holística, que en palabras de Boscán (2011) citado por Tacca et al. (2019) tendría de los tres tipos de estrategias neurodidácticas: las estrategias operativas, las estrategias socio-emocionales y las estrategias metodológicas; las que están compuestas por procedimientos que promueven la indagación, análisis y construcción del conocimiento mediante procesos lógicos y con apoyo de las otras estrategias: las operativas y las socio-emocionales.
El utilizar los cromos de situaciones del contexto y de fotos de los mismos estudiantes, se constituyó en un factor de motivación y compromiso para resolver los problemas, dado que estaban familiarizados con las situaciones y les emocionaba tener las fotos de sus compañeros. En esta línea de trabajo se inscribe la idea “una práctica de enseñanza adquiere real importancia cuando se reconoce atravesada por el contexto en el cual se desarrolla” (Fripp, 2012, p. 60), aun a pesar de que hay docentes que sostienen que el contexto no favorece medularmente al método de enseñanza.
La estrategia de Pólya se difunde desde la segunda mitad del siglo pasado, con aplicaciones en muchos países para el aprendizaje de muchos dominios temáticos y habilidades, principalmente las relacionadas con la resolución de problemas. También es notoria la tendencia de las investigaciones, que siguen utilizando su estrategia para resolver problemas, que se adicionan a la estrategia el uso de material didáctico como por ejemplo las regletas de Cuisenaire o material lúdico como el Dominó o el Ludo (con adaptaciones para usarlos en las sesiones de matemática), y en los últimos años la estrategia de Pólya con el uso de TIC (calculadoras, pizarras interactivas, diapositivas, el uso de internet, …), de software y Apps de matemática como el Geogebra o Graphmatica (Ministerio de Educación Nacional de Colombia, 2006; Murillo et al., 2016).
Docentes, de países como Ecuador y Colombia, que desarrollaron sesiones de aprendizaje utilizando la estrategia de Pólya, como parte de sus investigaciones, consiguieron que sus estudiantes, de diversos grados en primaria y secundaria lograran desarrollar la competencia/capacidad de resolución de problemas (Oliveros et al., 2021; Sánchez & Valencia, 2021; Villacis, 2021). Incluso la información recopilada a través de la observación y entrevistas, en una investigación cualitativa, indica que cuando utilizaron la estrategia de Pólya, los estudiantes comprendían mejor el problema y su desempeño de resolutor era mejor (Morales, 2021). Las conclusiones a las que arribaron tienen un correlato con el hecho de que lo general de la estrategia de Pólya son sus fases de desarrollo, que se adaptan muy bien a cualquier tipo de problema, de cualquier dominio temático y en cualquier nivel educativo, sea inicial, primaria, secundaria o superior. Las fases son:
a) comprensión del problema;
b) diseño de un plan de resolución;
c) ejecución del plan y;
d) revisión de lo desarrollado. Iguales resultados se obtuvieron en el Perú en diversas regiones como Puno, Junín y Lima (sierra y costa).
Las investigaciones refieren que los docentes lograron desarrollar la competencia/capacidad de resolución de problemas, con diversos temas, en diversos grados, utilizando en sus sesiones de aprendizaje la estrategia de Pólya (Lazo, 2017; Meneses & Peñaloza, 2019; Vilca et al., 2021).
Aun con la comprobación extendida en diversos países sobre los atributos de la estrategia de Pólya en el desarrollo de las competencias de resolución de problemas aún se sigue indagando sobre ello, así por ejemplo hay quienes toman como premisa que la resolución de problemas es la vía principal para aprender matemática, en general (Mendoza, 2022). Si en las investigaciones descritas se considera como causa a la estrategia de Pólya y al efecto a la resolución de problemas, hay quienes consideran que el resolver problemas es la causa (variable independiente) del efecto que sería el desarrollo de la competencia/capacidad de resolución de problemas, vale decir la resolución de problemas como método, como propósito y también como actividad.
Como variantes de las investigaciones que tienen como propósito que sus estudiantes aprendan a resolver problemas, son las que se refieren al uso de diferentes estrategias en las que utilizan diversos tipos de materiales para manipular, como en el caso nuestro. En otra clasificación se encuentran los juegos, algunos se convierten en retos graduales y otros que enfatizan la diversión combinada con el razonamiento matemático (Hurtado et al., 2020; Poma, 2022).
Otro tipo de investigaciones para lograr que los estudiantes sean buenos resolutores de problemas son las que utilizan como variable independiente a las heurísticas (Dionisio, 2017). Las heurísticas son referidas por el mismo Pólya como la estrategia que permite resolver problemas y que estas son aplicables independientemente del contenido involucrado en el problema (Boscán & Klever, 2012). Algunas heurísticas son: empezar considerando posibles respuestas, fraccionar el problema, ensayo-error, entre otras. Pero hay otras técnicas, que análogamente a la estrategia de Pólya, están constituidas por procedimientos matemáticos como, por ejemplo, las técnicas del rombo, del rectángulo, de la falsa suposición, de las representaciones gráficas del problema, entre otras, que encajan en la definición de técnicas matemáticas y que se utilizan de acuerdo con la naturaleza del problema.
Describiendo la estrategia de Pólya, diremos que nos brinda una estructura de cuatro fases, para tratar de encontrar la solución a un problema matemático, pero cabe mencionar que no siempre será el mismo camino, puesto que cada persona tiene diferentes formas de resolver los diferentes tipos de problemas. Lo que se pretende con estas fases es que el estudiante pueda orientarse de manera segura y correcta en la resolución de problemas, tratando de reducir el error y aumentando la significancia del proceso de aprendizaje al momento de enfrentarse a los problemas matemáticos (Pólya, 1969).
a. Comprensión del problema
Esta fase tiene mucha relevancia porque es difícil pretender resolver algo que no se entiende, por tal motivo el docente debe orientar a los estudiantes para que puedan identificar los elementos del problema y la relación que hay entre estos. Además, el docente tiene que seleccionar bien el problema ni muy fácil, ni algo que no puedan desarrollar los estudiantes, debe ser interesante, factible de poder ser resuelto en el tiempo que duran las clases (Pólya, 1969).
En esta fase se traza como propósito entender el enunciado, el estudiante debe reconocer la incógnita, los datos y la condición. Se orienta dicho proceso con preguntas como: “¿Qué es lo desconocido?, ¿Cuáles son los datos?, ¿Cuál es la condición?” Pólya (1969). Si hubiera alguna figura, la descripción del problema debe apoyarse en esta y si fuera necesario podría ubicarse los datos en esta también (Pólya, 1969).
b. Concepción de un plan
En esta fase se diseña la estrategia para resolver el problema. Lo ideal es que el estudiante con sus propios recursos pueda idear este plan. Podrá intentar de diferentes formas hasta que dé con el camino adecuado para la resolución. El docente debe mediar con preguntas y sugerencias: ¿Cómo resolviste algún problema parecido?, ¿Conoce un problema relacionado? Pero luego de ello, surge otro problema porque llegan a mente diversos problemas anteriormente resueltos y no sabemos cuál utilizar. Por tal motivo, no debemos olvidar el objetivo, que es encontrar la incógnita y debes de buscar un problema familiar que tenga la misma o similar incógnita. Para evitar que los problemas relacionados los desvíen del objetivo de resolver el problema formulado, el docente debe encauzar nuevamente con las siguientes preguntas: ¿Usó todos los datos?, ¿Usaste toda la condición? (Pólya, 1969).
c. Ejecución del plan
Ejecutar el plan es relativamente fácil. Para no hacer una mala ejecución el estudiante debe percatarse que todos los datos estén en el esquema, examinar que todo esté correctamente escrito y encajado en su debido lugar. El docente debe insistir en que el estudiante verifique que todo esté correcto. Al ejecutar el plan, el estudiante debe tener cuidado de proceder correctamente. Para ello Pólya propone dos interrogantes: ¿Puedes ver claramente que el paso es correcto? y ¿puedes probar que el paso es correcto? (Pólya 1969).
d. Visión retrospectiva
Antes de dar por terminada la resolución del problema y pasar a resolver otro, si lo hubiera, los estudiantes deben acostumbrarse a revisar el procedimiento realizado y examinar el resultado. El docente debe recalcar que ningún problema está totalmente terminado, siempre puede haber alguna falla por algún calculo rápido-intuitivo o reestructurarlo de otra forma más sencilla. Para ello Pólya propone dos interrogantes: ¿Se puede verificar el resultado? y ¿Puedes justificar tu procedimiento y resultado? (Pólya, 1969).
Recursos y materiales didácticos
Se parte de la premisa de que se concibe a los recursos educativos como todo material que agiliza y mejora los procesos de enseñanza y aprendizaje. Pueden presentarse de forma virtual como de forma física. Cumple dos funciones principales: en primera instancia genera interés de los estudiantes y la otra función es que facilita la praxis del docente (Vargas, 2017, p. 69). El material didáctico, formando parte de los recursos didácticos, es aquel que brinda apoyo a los procesos de enseñanza y aprendizaje, permitiendo al docente, consolidar en los estudiantes su percepción y análisis del objeto de aprendizaje por medio del material brindado por el docente. Caamaño et al. (2021) también hace suya la idea de que una de las propiedades de los materiales didácticos es la que puede usarse para representar hechos de situaciones, procesos o fases reales con la finalidad de dar oportunidades al estudiante para una detallada y mejor observación, para desarrollar en él la capacidad de análisis y que también se usa para “estimular la memorización de los conocimientos y desarrollar las habilidades de ubicación temporal y espacial, y son favorecedores de la asimilación consciente, rápida y eficaz de los contenidos curriculares” (pp. 319-320).
Cotton et al. (1995) confrontan dichas definiciones, destacando el rol profesional del docente: manifiestan que en los países que tienen buen nivel de logro, los recursos educativos no tienen una relación significativa con respecto al rendimiento académico de los estudiantes, puesto que la eficacia de estos recursos depende mucho de los docentes que los utilizan. Así también, Hanushek (1986) ya mencionaba, en esa época, que los buenos resultados en los logros de los estudiantes dependían de que estos y los docentes eran mejores y no de que la institución educativa cuente con buenos recursos educativos. Casi 20 años después en un trabajo con Luque en el 2003 citado por Murillo et al. (2016, p. 3) indican “que disponer de estos recursos (educativos) no siempre mejora los desempeños escolares”. Situación similar, de dilema en el rol de los recursos educativos, a nivel de países, describen las investigaciones, que derivan en la afirmación, que en países desarrollados la relación entre los recursos educativos y el aprendizaje no es significativa, mientras que en países menos desarrollados existe mayor significancia, vale decir que una alta gama de recursos educativos está asociada positivamente al rendimiento académico (Dee, 2005; Flaherty, 2013; Greenwald et al., 1996; Velez et al., 1994).
Nosotros nos alineamos con las investigaciones que, entre otras conclusiones, refieren que los recursos educativos son factores importantes para un buen rendimiento académico. Investigaciones como la de Betts y Shkolnik (2000) que contrastaron la tenencia y uso de recursos educativos, llegan a la conclusión de que instituciones educativas con carencia de recursos educativos tienen un menor rendimiento académico.
El uso de material didáctico en la enseñanza de las matemáticas ha sido ampliamente estudiado, tanto de materiales concretos como virtuales. Hay evidencia de que el uso de material didáctico mejora el aprendizaje de contenidos y conceptos matemáticos, así también, que desarrolla habilidades relacionadas con dicho aprendizaje. Además, la experiencia directa de manipular objetos didácticos permite una mayor comprensión de conceptos que se convierten en la base del conocimiento matemático conceptual y abstracto. Asimismo, la UNESCO (1998) en uno de sus documentos académicos menciona que con el uso de material didáctico se aprende mejor letras y matemática. Son más, en el área de Matemática, las investigaciones que ponen en alto relieve, la contribución con el aprendizaje, el uso de recursos didácticos en las sesiones de aprendizaje: “Entre los efectos reportados se constata mejora del aprendizaje de contenidos y conceptos matemáticos, así como el desarrollo de habilidades implicadas en dicho aprendizaje” (Reimer & Moyer, 2005; Román et al., 2006; Steen et al., 2006 citados por Murillo et al., 2016, p. 5). Al utilizar recursos educativos en las actividades de aprendizaje, además de motivar y dirigir la atención hacia lo que desean aprender los estudiantes, permiten que ellos estructuren mejor las ideas y la comprensión de los objetos de aprendizaje y la ejercitación de los procedimientos para resolver una situación, que en el caso de las matemáticas son problemas relacionadas con las competencias del área y con el desarrollo de los distintos tipos de pensamiento matemático (Ministerio Educación Nacional de Colombia, 2006).
A nivel de instituciones que dirigen el funcionamiento de los sistemas educativos de países, en especial en el área de Matemática, recomiendan que en las secuencias didácticas se incorpore el uso de material didáctico, así por ejemplo en Argentina recomiendan que hagan uso de calculadoras, material concreto como el geoplano y en general el uso de recursos didácticos de contenidos variados que complementen la tarea de enseñanza del docente, mientras que en Colombia en palabras similares fundamentan el uso de los recursos didácticos porque a través de estos se pueden proponer retos, romper lo rutinario de la sesión, fomentar la diversidad de representaciones, facilitando que los estudiantes se enfoquen en procesos de razonamiento propios de las matemáticas (Ministerio de Educación de la Nación Argentina, 2019; Ministerio de Educación Nacional de Colombia, 2006).
Álbum-Mátic
Como manifiesta el Ministerio de Educación Nacional de Colombia (2006, pp. 74-75), el Álbum-Mátic (A-M) se clasifica como un recurso didáctico, bajo la premisa de que los recursos didácticos, son todos los materiales físicos o virtuales que permiten motivar, generar retos, brindar información, facilitar la comprensión, o como soporte de la secuencia didáctica que sirven de base para estructurar los problemas alineados a la situación significativa que se haya seleccionado (ver Figura 1).
Al ser el A-M un recurso didáctico adaptado de un pasatiempo tradicional (para algunos un juego de duración larga) de los niños y jóvenes, que se integra a la estrategia de Pólya, que por definición es activa, aplican en estos los fundamentos de la neurociencia (los que corresponden), que fueron extrapolados a la didáctica en 1988 por Gerhard Preiss, generando un ámbito de investigación: la neurodidáctica. Hoy se sabe, por esta disciplina científica: a) que se aprende mejor cuando esta tarea, la de aprender, se desarrolla en forma activa en equipos de trabajo, en forma colaborativa; b) que, si la acción didáctica se desarrolla lúdicamente, genera en los estudiantes un interés que implica motivación e involucramiento voluntario en las actividades de aprendizaje, favoreciendo a que el aprendizaje sea significativo.
De igual manera se sostiene que material como el A-M que tiene presentación virtual y física, así como que retroalimenta, de acuerdo a las dificultades, a través de códigos QR conectados a la plataforma de videos Youtube, permite convertir el aula tradicional en aula virtual, favoreciendo la variedad de la sesión y además, el uso de otros recursos tecnológicos, para mantener motivado a los estudiantes durante todo el desarrollo del proceso, involucrándolos en el trabajo con acuerdo a su propio ritmo de aprendizaje (Lázaro & Mateos, 2018).
Competencia matemática
Algunas definiciones de las competencias del área de Matemática giran en torno a la idea de que es una capacidad para utilizar recursos internos y externos (cognitivos y tecnológicos) en la resolución de problemas cotidianos, científicos o tecnológicos, debidamente contextualizados, en forma idónea (López et al., 2021; Minedu, 2016), a ello se añade que su logro necesita de un escenario y situaciones de reto que sean de interés de los estudiantes (Ministerio de Educación Nacional de Colombia, 2006).
Las definiciones de los propósitos de la matemática sean estos desarrollo/logro de competencias o capacidades, tienen lugares comunes en los países de América del Sur: a) uso de los saberes en la solución de problemas cotidianos del entorno y los disciplinares de la ciencia matemática y; b) desarrollo del área aplicando y desarrollando capacidades y procedimientos relacionados con el razonamiento, la comunicación y argumentación. Así por ejemplo nos dicen que aprendemos matemática desarrollando la capacidad de razonar y resolver problemas matemáticos en situaciones cotidianas, en contextos científicos y tecnológicos, de igual manera, agregan que dichos procesos involucran el uso de conceptos, procedimientos, técnicas y herramientas matemáticas (Arreguín et al., 2012; Ministerio de Educación de la Nación Argentina, 2019; Mineduc-Chile, 2023; Minedu, 2016).
En el Perú las competencias del área curricular de matemática tienen como marco, enfoque y eje la resolución de problemas. La resolución de problemas en cuatro dominios temáticos relacionados con los conjuntos numéricos, las relaciones y expresiones algebraicas, la geometría y la estadística. Sobre la resolución de problemas se manifiesta la idea coincidente con la de Valbuena et al. (2020) que definen la resolución de problemas como procesos por los cuales los educandos aprenden a pensar matemáticamente, desarrollan habilidades, destrezas y competencias (Minedu, 2016). En el discurso enfatizan lo que sostiene Pólya (1969) acerca de las cuatro etapas que se tiene que transitar para resolver problemas y lo que plantea Schoenfeld (1992) citado por Albornoz (2022) de que las heurísticas no bastan para ser un buen resolutor, hay la necesidad de otros factores.
Capacidades matemáticas
Las capacidades matemáticas son las destrezas y habilidades que una persona necesita para comprender y aplicar los conceptos y principios de las matemáticas. Los Ministerios de Educación de Argentina, Chile, Colombia y Perú definen así las capacidades, respectivamente: “(…) la capacidad cognitiva general de resolución de problemas que consiste en la solución de situaciones que resulten desafiantes para el estudiante requiriendo reinvertir los conocimientos matemáticos disponibles” (Ministerio de Educación de la Nación Argentina, 2019, p. 10), en Chile, en un documento oficial, en referencia a la matemática no hablan de capacidades, como en el Perú, sino de “desarrollo de habilidades (resolver problemas, modelar, representar, argumentar y comunicar) para potenciar el pensamiento y el razonamiento matemático” (Mineduc, 2018, p. 32), de manera diferente, pero con descriptores semejantes, manifiestan en un documento educativo oficial colombiano, que desde el 2006 orienta la elaboración curricular en las instituciones educativas, que son “cinco procesos generales que se contemplaron en los lineamiento curriculares de matemática: formular y resolver problemas; modelar procesos y fenómenos de la realidad; comunicar; razonar, y formular comparar y ejercitar procedimientos y algoritmos” (Ministerio de Educación Nacional de Colombia, 2006, p. 51), y en el Perú “Las capacidades son recursos para actuar de manera competente. Estos recursos son los conocimientos, habilidades y actitudes que los estudiantes utilizan para afrontar una situación determinada. Suponen operaciones menores implicadas en las competencias que son operaciones más complejas” (Minedu, 2016, p. 30). Las capacidades en el área de Matemática, en el Perú son cuatro:
a) Traducir situaciones cotidianas a expresiones matemáticas;
b) Comunicar ideas matemáticas;
c) Utilizar estrategias y;
d) Argumentar matemáticamente procesos y procedimientos, dependiendo su concreción del dominio de la competencia.
En general, se puede afirmar que las definiciones señaladas concuerdan en la importancia de la resolución de problemas y la comunicación matemática.
Método y material
a. Método
Se siguió la ruta cuantitativa, con un diseño cuasiexperimental con grupos control y experimental, con pruebas de entrada y salida. La población estuvo constituida por 120 estudiantes del 1ro. de secundaria de la institución educativa San Vicente de Paul-Jauja, considerándose 60 alumnos de dos secciones para la muestra, de los cuales 30, de una sección, fueron del grupo experimental y los restantes, de la otra sección, del grupo control, quedando establecida la técnica de muestreo de grupos intactos, en la que los estudiantes no se asignaron al azar a algunos de los grupos ni se emparejaron ni fueron agrupados expresamente para el experimento (Hernández-Sampieri & Mendoza, 2018).
b. Validez y confiabilidad del instrumento
Las pruebas de entrada y salida, ambas de 8 ítems, fueron validadas en su contenido por cinco expertos, quienes por unanimidad dieron el veredicto de que se aplique sin modificación alguna. Las pruebas de entrada y salida estuvieron constituidas por problemas del mismo nivel de dificultad y que exigían desempeños similares, de los estudiantes. También se aplicó una prueba piloto a 20 estudiantes, cuyos resultados fueron procesados con el estadístico alfa de Cronbach, cuyo coeficiente fue de 0,765, valor que indica confiabilidad: “(…) valor mínimo de 0,70 para la comparación entre grupos (…)” (Lauriola, 2003 citado por Hernández-Sampieri & Mendoza, 2018, pp. 324-325).
c. Material
El A-M que se utilizó en la investigación tiene la forma y volumen de un cuaderno tamaño carta, similar a los comics, con pasta blanda. En las hojas que la constituyen hay recuadros con información breve sobre el mensaje o contenido de las fotos que se deben pegar, las fotos (los cromos) son de los estudiantes que participaron en el experimento y de actividades económicas, sociales y culturales de la provincia.
Los problemas que se plantearon en el A-M se formularon para desarrollar las competencias de resolución de problemas de cantidad, regularidad, equivalencia y cambio, contextualizados a las actividades económicas de Jauja, tales como: a) Agricultura; b) Turismo; c) Comercio y; d) Cultura; utilizando procedimientos de las técnicas de Falsa suposición, El Cangrejo, Regla conjunta y El Rectángulo; para resolver problemas.
Los estudiantes participaron en una competencia de resolución de problemas para ganarse las fotos para llenar antes que los demás el A-M. Ganaban quienes completaban primeros el álbum. En cada sesión el docente medió las actividades de los equipos de estudiantes para que puedan resolver los problemas, transitando por las fases de Pólya y así poder sustentar sus respuestas o soluciones. Los equipos que no lograban resolver los problemas indicados solicitaban al docente el QR vinculado a un canal de videos Youtube con la resolución de los problemas propuestos (ver Figura 2), de modo tal que los estudiantes con dificultades podían ver en casa los videos de resolución de los problemas, con la finalidad de retroalimentar lo trabajado y cerrar brechas entre lo enseñado y aprendido. Al finalizar cada sesión, se realizaba la metacognición, enfocada al trabajo de cada equipo. Luego se les pedía crear problemas matemáticos de las temáticas de la sesión para que los estudiantes activen su creatividad. La distancia, en tiempo, de la prueba de entrada y salida, que es el tiempo total de la experimentación, fue de dos meses.
Resultados y discusión
a.Análisis descriptivo de la prueba de entrada
En general, como se observa en la Tabla 1, los estudiantes de ambas secciones mostraron un bajo rendimiento. Solo 5 de 60 estudiantes aprobaron. Además, los promedios de los primeros C y D son respectivamente, 9.23 y 7.97, por lo que se determinaron como grupos control y experimental al primero C y D, respectivamente.
b. Análisis descriptivo de la prueba de salida
Posterior al trabajo con la estrategia Pólya con el A-M en el grupo experimental, se aplicó una prueba de salida, cuyos resultados se observan en la Tabla 2:
Tabla 2: Prueba de salida-Grupos control y experimental
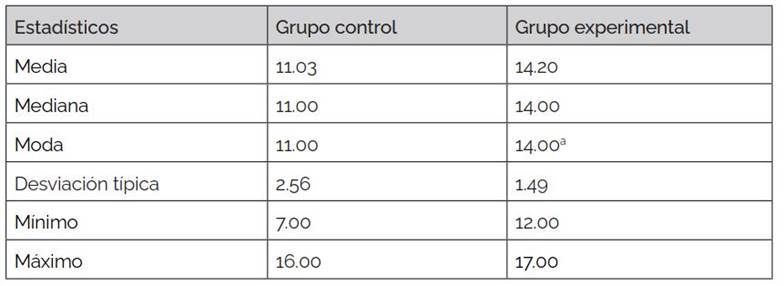
Nota. a: Existen varias modas. Se muestra el valor más pequeño.
Se observa una diferencia de 3.17 en la media, a favor del grupo experimental. Además, en el grupo experimental el puntaje máximo es mayor y la desviación típica es menor, que en el grupo control.
c. Pruebas de hipótesis
Con una distribución normal de los resultados de la prueba de salida, a un nivel de significancia de 0.05, con el estadístico t de Student, se obtuvieron los siguientes resultados (ver Tabla 3):
Tabla 3: Pruebas de hipótesis específicas y general
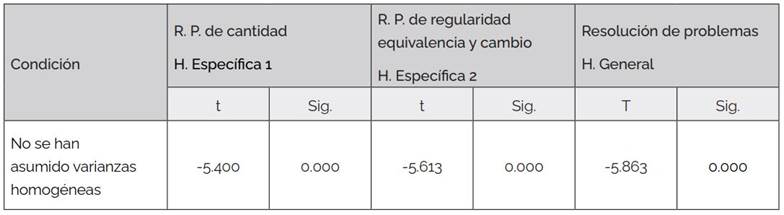
Nota. R. P.: Resolución de problemas; H.: Hipótesis.
En las pruebas de resolución de problemas de cantidad, resolución de problemas de regularidad, equivalencia y cambio, así como en la competencia resuelve problemas, tal como se observa en la Tabla 3, los p-valor (Sig.) son menores a 0.05 por lo que se deduce que existe evidencia estadística que la diferencia de medias es significativa, a favor del grupo experimental.
El desarrollo de las sesiones de aprendizaje siguiendo las fases de la estrategia de Pólya, implicó desarrollo del pensamiento de los estudiantes, exigido por la necesidad de comprender el problema y diseñar un plan de resolución de problemas. La calidad de esta actividad del pensamiento es la resolutora de los problemas y la evidencia se expresa estadísticamente en los resultados, en los que se aprecian diferencias significativas en los calificativos de los grupos de estudiantes que recibieron las sesiones de aprendizaje con la estrategia de Pólya en referencia a los que las recibieron. Los resultados coinciden con los obtenidos por otros investigadores como Oliveros et al. (2021), Sánchez y Valencia (2021) y Villacis (2021).
La muestra de estudio estuvo constituida por estudiantes del primero de secundaria y en ellos, la aplicación de la estrategia de Pólya tuvo buenos resultados, sin embargo, similares resultados se obtuvieron en diferentes niveles educativos, esto implica que se puede emplear la estrategia de Pólya, graduando pertinentemente la complejidad de los problemas, así lo corroboran Lazo (2017), Meneses y Peñaloza (2019) y Vilca et al. (2021).
Utilizar material didáctico en las sesiones de aprendizaje es un factor que otorga más probabilidades de éxito en el cumplimiento de los propósitos de la sesión, dependiendo de los atributos que los estudiantes encuentren en el material. Muchas investigaciones convienen que la estrategia de Pólya per se garantiza, en el ámbito de la resolución de problemas matemáticos, el desarrollo de las capacidades y competencias relacionadas con la resolución de problemas. Pero la variedad de formas de aplicar el método, presentando material didáctico o utilizando recursos tecnológicos, potencia la motivación y el involucramiento en las tareas de resolución de problemas. En nuestro caso, se integró al desarrollo de la estrategia de Pólya el uso del A-M, obteniendo una motivación especial dada por su doble característica, de ser un material lúdico y el de promover una competencia sana de llenar el A-M rápidamente y para lograr ello tenían que resolver los problemas más rápidamente. Existen ejemplos de resultados similares, en investigaciones recientes, en las que se utilizaron material didáctico como juegos de mesa y recursos tecnológicos como el GeoGebra. Estos hechos y la importancia de utilizar material didáctico han sido difundidos por el Ministerio de Educación Nacional de Colombia (2006) y Murillo et al. (2016) y, como sentenciará Murillo et al. (2016, p. 17): “(…) los recursos sí importan (…). Negar este hecho (…) solo contribuye a postergar la posibilidad de una educación más equitativa y de mayor calidad”. Estas ideas compatibles con las nuestras no quitan el valor de las que derivaron de investigaciones, que minimizan el rol del uso de material en la mejora de la calidad de los aprendizajes de los estudiantes (Cotton et al., 1995; Hanushek, 1986), solo que los objetivos de estas tuvieron como centro la relación inversión-resultados o equipamiento-resultados, dejando marginalmente, el proceso mismo del aprendizaje, que es previo al resultado y tan importante como este.
Conclusiones
La aplicación de la estrategia de Pólya utilizando el A-M favoreció el aprendizaje de la competencia resuelve problemas, en los estudiantes del grupo experimental, tomando como referencia los estudiantes que no desarrollaron sus sesiones de aprendizaje con la estrategia de Pólya ni con el A-M. De igual manera fueron significativas las diferencias, a favor, de las medias de los estudiantes del grupo experimental en la prueba de salida sobre las competencias resuelve problemas de cantidad y resuelve problemas de regularidad, equivalencia y cambio.
La estrategia de Pólya es amigable para los estudiantes. Estos, siguieron la rutina del pensamiento de resolución de problemas de forma natural, se enfocaron en el problema para determinar, el tipo de problema, los datos, las características de la pregunta y la forma en que se deberían relacionar o integrarlos en algún esquema, ecuación o procedimiento matemático.
El Álbum-Mátic fue un material motivador para que los estudiantes desearan resolver los problemas en clase y aprendieran a hacerlo, evidenciándose ello en los resultados de la evaluación de salida.