Introducción
La demanda de energía de la edilicia existente, se puede reducir considerablemente actuando sobre la eficiencia energética de su envolvente, revalorizando e incorporando atributos termo-físicos de su materialidad (Ministerio de Ciencia, Tecnología e Innovación 2022). Para ello es necesario reconocer y recuperar, a partir de pautas de reciclado edilicio y eficiencia energética (EE), la materialidad como una masa de acumulación térmica, que puede aprovecharse como almacenamiento de energía de base para sostener los niveles térmicos de habitabilidad esenciales.
En la Argentina, el porcentaje de participación de las energías renovables en la matriz energética es pequeño comparado con el de centrales térmicas, que es del 58,9% (CAMMESA 2022) generado a partir de fuentes no renovables. Por lo tanto, la reducción del consumo energético resulta fundamental si se quieren cumplir metas relacionadas con la disminución de emisiones de gases de efecto invernadero, a las que el país ha adherido. Para alcanzar tales metas, es imprescindible accionar sobre el uso eficiente de la energía y sobre la envolvente de la edilicia existente de manera sistémica y masiva aplicando criterios de intervención y selección de sistemas constructivos eficaces, eficientes y acordes a las realidades presupuestarias locales. Ante esta situación es necesario actuar sobre la demanda de energía, principalmente a través de políticas que incidan sobre el uso final de la energía en el sector construido a través de estrategias, metodologías y herramientas que permitan evaluar, dimensionar y actuar sobre la edilicia existente, mejorando la eficiencia energética de su envolvente.
Desde el punto de vista del consumo final de energía en el año 2020 se observa que aproximadamente el 34,67% de la matriz energética nacional corresponde a los Sectores Residencial y Comercial-Público (Ministerio de Economía 2024). Dentro de este último Sector se incluye el subsector Salud. Los edificios de este subsector se caracterizan por ser energo-intensivos debido a su infraestructura de uso continuo y equipamiento (Urteche et al, 2021). De allí el interés en analizar en este trabajo un edificio de este sector. Por otro lado, el reciclaje sistematizado de la edilicia existente y su aplicación masiva, a partir de propuestas tecnológicas pasivas avaladas por una metodología de selección multicriterio que permita evaluar sus cualidades técnicas y económicas, representa una alternativa viable para intervenir en la envolvente de los edificios y sus sistemas constructivos. En este sentido, este trabajo propone analizar, utilizando un enfoque multicriterio, diferentes alternativas tecnológicas constructivas para el mejoramiento de la eficiencia de la envolvente edilicia del subsector salud, que contribuyan a lograr ahorros en términos de consumo de energía, al mismo tiempo que se mantienen (y eventualmente mejoran) las condiciones de habitabilidad, el confort higrotérmico, la calidad de vida y los aspectos ambientales.
Entre la bibliografía sobre antecedentes similares al trabajo que se presenta, se encuentran los aportes de los autores que se mencionan a continuación.
En el trabajo de Álvarez et al. (2018), se intenta optimizar el ciclo de vida de los materiales de los sistemas constructivos presentes en zonas áridas-sísmicas mediante un proceso analítico jerárquico para determinar los pesos de tres criterios (energía para la producción y el transporte, emisiones de CO2 y transmitancia térmica) y evaluar las diferentes partes de la envolvente (muros, aberturas y techo). Así como en el trabajo anterior Donnarumma et al. (2017), utilizan el proceso analítico jerárquico aplicado a tres criterios (rendimiento energético, desempeño de sostenibilidad y costo). Para determinar el peso de cada criterio se tuvieron en cuenta tres grupos de personas, entre las que se encontraban: administradores públicos, inversores privados y técnicos. Estas personas determinaron los pesos de los criterios que luego formarían parte de un índice que los agrupó llamado Índice de modernización energética y sostenibilidad ambiental. De manera similar, Ongpeng et al. (2021) utilizan un proceso analítico jerárquico (AHP) para determinar los pesos de los indicadores que luego son utilizados por el método VIKOR. Los indicadores pertenecen a tres categorías: i. ambiental, ii. económico y iii. técnico. Este método calcula la bondad de las alternativas en función de su proximidad a la situación ideal. Para el cálculo de la distancia, utiliza la distancia de Manhattan y la de Chebyshev como métricas, en lugar de la euclidiana.
Azar (2001) propone el uso de un algoritmo genético para optimizar la envolvente del edificio en función del costo y el rendimiento energético durante la etapa de prediseño. Previo a utilizar el algoritmo genético, cada actor que participa o influye de alguna manera en el diseño de la envolvente (ej.: el propietario) debe expresar sus preferencias para poder asignar pesos a los diferentes criterios. Se evalúa el desempeño energético y de costos de todos los escenarios definidos por los actores (un actor puede definir más de un escenario). El software puede realizar un análisis de sensibilidad para observar el resultado de las dos variables de interés cambiando el valor de los parámetros (que expresan preferencias). A diferencia de este trabajo, en Moschetti et al. (2022) no consideran la opinión (preferencias) de expertos u otros actores. En su lugar, se utilizan tres índices: demanda anual de energía, porcentaje de horas de confort térmico y factor de carga. Las diferentes alternativas se evalúan mediante el método minimax. Por último, en Romani et al.(2022) se analizan diferentes alternativas de reciclaje de edificaciones en el sector residencial considerando dieciséis criterios organizados en tres grupos: i. necesidades de energía para calefacción, ii. económico, iii. ambiental.
Este trabajo presenta una metodología basada en un enfoque multicriterio orientada a evaluar estrategias de reciclado edilicio a partir de propuestas tecnológicas que consideren cualidades técnicas y económicas en el marco (de las pautas) del diseño pasivo. A diferencia de los trabajos anteriores, la metodología aquí propuesta considerará 2 criterios y no utilizará ningún método para determinar el valor de los pesos asociados a cada criterio (ej.: AHP, panel de expertos) sino que se estudiará cual es la alternativa más conveniente para cada posible valor con que se pondere a cada criterio.
Metodología
La metodología de evaluación multicriterio es particularmente útil en problemas vinculados con el desarrollo sustentable (Hersh 2006). Esto se debe, en gran medida, a su capacidad para describir un objeto de estudio como un vector compuesto por diferentes criterios que suelen estar en conflicto entre sí. En particular, en la arquitectura generalmente ocurre que las “mejores alternativas” suelen ser las menos económicas. Ante este tipo de problemas, donde se desea tener en consideración todos los criterios a la vez para optar por una de entre varias alternativas, la utilización de la metodología de evaluación multicriterio es particularmente apropiada (Coello Coello 2003).
La metodología de evaluación multicriterio consta de las siguientes etapas:
Etapa 1: Se definen los criterios relevantes acerca de los objetos o alternativas que interesa comparar.
Etapa 2: Para cada una de las alternativas a evaluar, se deben conocer los valores correspondientes de cada criterio y se procede a escribirlos en forma matricial.
Etapa 3: Se comparan todos los posibles pares de alternativas y se eliminan aquellas que resulten ser alternativas (o soluciones) dominadas. A tal efecto se utiliza el criterio de dominancia de Pareto, el cual señala que una alternativa A domina a otra B, si existe al menos un criterio en que la alternativa A supera (en forma estricta) a B, y en el resto de los criterios, los valores de cada criterio de la alternativa A no “pierden” con los correspondientes de B.
Si existen N alternativas posibles, entonces la función que señala el número de pares de alternativas que se deben comparar entre sí viene dada por f(N)=(Nx(N-1))/2 . Esto se debe a que cada una de las N alternativas se compara con las restantes N-1. La división por 2 se debe a que comparar una alternativa a con otra b es lo mismo que comparar a la b con la a de modo que se debe contar este hecho una sola vez.
Etapa 4: Se normaliza cada criterio y se reescribe la matriz anterior con valores normalizados. En este punto sólo quedan las alternativas no dominadas. Estas alternativas son todas igualmente buenas en el sentido de que no se puede decir que haya una mejor que otra. Es decir, para una alternativa dada, no existirá otra que la domine en el sentido de Pareto.
Así, pues, en esta etapa se analiza cada criterio para ver si valores más altos reflejan una situación más favorable o si son los valores más bajos los que reflejan una situación mejor para luego normalizarlos. Esto da lugar a la aplicación de dos fórmulas diferentes, según sea el caso:
Caso 1: en caso de que valores menores reflejen una mejor situación se procede a normalizar tal criterio siguiendo la fórmula:
f(x)=(MÁXIMO-x)/(MÁXIMO-MÍNIMO)
donde:
MÁXIMO: es el máximo valor del criterio teniendo en cuenta los valores de su propia columna para todas las alternativas.
MÍNIMO: es el menor valor en esa misma columna.
Caso 2: en caso de que valores mayores reflejen una mejor situación se procede a normalizar el criterio siguiendo la fórmula:
f(x)=(x-MÍNIMO)/(MÁXIMO-MÍNIMO)
donde:
MÁXIMO: es el máximo valor del criterio teniendo en cuenta el valor de su propia columna para todas las alternativas.
MÍNIMO: es el menor valor en esa misma columna.
Resulta importante recordar que, en ocasiones, el valor máximo y mínimo pueden ser valores teóricamente posibles pero no alcanzados por las alternativas que se están analizando. Por ejemplo, suponiendo que se están comparando 2 ciudades y hay un criterio que es "% de hogares con agua potable por red", si un municipio tiene el 77% y el otro un 78%, y dado que lo deseable es que la cobertura fuese del 100%, si se normaliza con MÁXIMO=78 y MÍNIMO=77 resultará que luego de la normalización, el municipio con 78% tendrá el valor 1 (óptimo) en ese criterio y el otro municipio tendrá el valor 0, aún cuando su diferencia sea de un 1%. Una situación más realista sería normalizar con los valores MÁXIMO=100 y MÍNIMO=0 que serían los valores máximo y mínimo teóricos posibles (aunque ninguno de los municipios alcance tales valores). Así, si se sigue este principio, luego de la normalización un municipio tendrá un valor de 0,78 y el otro 0,77.
En síntesis, al normalizar, para cada atributo se pueden elegir los valores máximo y mínimo de las alternativas a analizar, o la otra forma posible de hacerlo es considerar los valores máximo y mínimo teórico (aunque estos valores no aparezcan en las alternativas a comparar). Por lo tanto, antes de adoptar la metodología se debe decidir cuál de las 2 formas es la que más se aproxima a la realidad.
Etapa 5: Se consulta a los usuarios y/o destinatarios y/o expertos acerca de la importancia que se debe asignar a cada uno de los criterios y se construye la función de preferencia.
En el caso de que las personas consultadas no tengan preferencias se puede dar como resultado las alternativas que llegaron a la etapa 4 o se puede suponer que todos los criterios tienen igual importancia y continuar con la etapa 5 y las siguientes. En caso de continuar con la etapa 5 y las siguientes, se debe proceder a crear una función que permita evaluar la aptitud de cada alternativa. Suponiendo que cada alternativa (representada por un vector X1,X2,…,XN) consta de N criterios, y que el peso de cada criterio es ci (i=1..N), entonces la función F que asigna un valor a cada alternativa es una construcción lineal ponderada cuya fórmula es:
N
F (X1,X2,…,XN) = Σ ci . Xi
i =1
En la fórmula anterior, la suma de los ci debe ser igual a 1. Así, si se tienen N criterios, y se desea asignar el mismo peso a cada uno, los valores de ci deberían ser todos igual a 1/N.
Etapa 6: Se aplica a cada vector de la matriz (cada alternativa) con valores normalizados, la función de preferencia para obtener una puntuación.
Etapa 7: Se elige la mejor alternativa y se construye un ranking ordenando las alternativas de mayor a menor según el puntaje obtenido al aplicarles la función de preferencia. Aquella alternativa con mayor valor será la mejor (óptima). La alternativa óptima podría no ser única si más de una alcanzan el mismo valor.
Si bien esta metodología puede ser utilizada en diversos sectores edilicios, es importante señalar que la misma puede abordar los aspectos de eficiencia energética así como los de sustitución de fuentes tradicionales por renovables. En este sentido, los criterios a tener en cuenta en cada caso son:
i. En el caso de aplicarse la metodología para evaluar alternativas de eficiencia energética se debe proceder, como señala el paso 1, a elegir los criterios relevantes que representarán a cada alternativa. En el inciso siguiente, se expone un ejemplo de la aplicación de la metodología para evaluar la EE donde los criterios que se tuvieron en cuenta fueron: la transmitancia térmica (K) y el costo de inversión inicial (CII) de diferentes muros.
ii. En el caso de aplicarse la metodología para evaluar alternativas de energías renovables (ER) no sería necesario incluir un criterio vinculado con el ahorro de energía pues el consumo se mantendría igual (ya que se trata de una sustitución de una fuente por otra de tipo renovable) y el beneficio debería medirse, por ejemplo, en términos de emisiones de CO2 evitadas. El costo de inversión inicial, no obstante, puede ser utilizado en cualquier caso (EE y ER).
Expuestas las particularidades para cada abordaje (EE y/o ER), se plantea aplicar dicha metodología en un ejemplo para evaluar las alternativas de eficiencia energética (EE) en un establecimiento de salud.
Resultados
A modo de ejemplo, se desarrolla el caso de aplicación de la metodología para la evaluación de la eficiencia energética (EE) de la envolvente de un edificio de salud. Como se señaló anteriormente, el diagnóstico y la implementación de medidas para el mejoramiento de la eficiencia energética constituyen el paso previo para la posterior sustitución de fuentes de energía convencionales por renovables.
La metodología se aplicará al caso del Servicio de Internación Clínica del Área de Internación del Hospital Zonal General de Agudos “Dr. Ricardo Gutiérrez”, el cual posee las siguientes características tecnológico-constructivas (figura 1). En el mismo gráfico se pueden observar también las propuestas de reciclado.
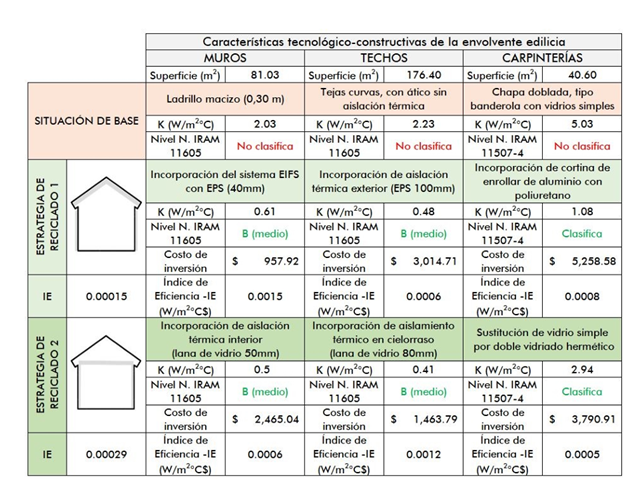
Figura 1: Ficha que contiene los datos necesarios para aplicar la evaluación multicriterio para la elección de diferentes alternativas tecnológico-constructivas para el reciclado de la envolvente edilicia
La figura 1 muestra que la envolvente edilicia se compone de superficies verticales, tanto opacas (muros) como transparentes (aberturas), y de superficies horizontales (cubierta). Así, es posible aplicar la metodología desarrollada para evaluar estrategias de reciclado edilicio que contemplen todas las partes simultáneamente (muros, aberturas y cubierta), o bien, evaluar cada parte por separado. En el ejemplo siguiente se evalúa una de las partes de la envolvente: los muros.
Caso: superficie vertical opaca - muros
Aplicando la metodología expuesta anteriormente se obtienen, en cada etapa, los siguientes resultados:
Etapa 1:
En esta etapa se especifican los criterios a tener en cuenta que serán 2: la transmitancia térmica (K) y el costo de inversión inicial (CII) de los diferentes muros.
Etapa 2:
Una vez definidos los 2 criterios, se procede a relevar sus valores para cada una de las 3 alternativas posibles (caso base, alternativa 1 y alternativa 2). Los valores de transmitancia térmica (K) en W/m2°C y de Costo de Inversión Inicial (CII) en $ son los que se observan en la figura 1.
Estos cálculos se realizan a partir de los datos de la ficha anterior, de la que se obtienen los valores de transmitancia térmica K (W/m2°C) y CII (costo de inversión inicial) para cada alternativa constructiva.
Caso base (alternativa constructiva 0): K=2,03. CII=0.
Caso reciclado 1 (alternativa constructiva 1): K=0,61. CII=957,92.
Caso reciclado 2 (alternativa constructiva 2): K=0,5. CII=2465,04.
Luego de calculados los valores de cada criterio para cada una de las alternativas, se procede a escribir esta información en forma matricial.
Etapa 3:
Dado que hay N=3 alternativas diferentes se deben comparar Nx(N-1)/2=3 pares de alternativas y ver si hay alguna dominada, en cuyo caso debe eliminarse.
Par 1: Se compara la alternativa 0 con la 1 y resulta que ambas constituyen soluciones no dominadas.
Par 2: Luego se compara la alternativa 0 con la 2 y resulta que ambas son no dominadas entre sí.
Par 3: Por último, se compara la alternativa 1 con la 2 y resulta que ambas son no dominadas.
A partir de las comparaciones anteriores se determina que no es posible eliminar ninguna alternativa pues, para cada par analizado, no se da el caso en que haya dominancia de Pareto de una alternativa respecto de la otra.
Etapa 4:
Se procede a normalizar cada uno de los criterios y reescribir la matriz con las alternativas que quedan (soluciones no dominadas), ahora, con valores normalizados. Para ello se utiliza, para cada criterio, la función:
f(x) = (MAX-x) / (MAX-MIN)
Esta función asigna valores (en el intervalo (0,1)) más altos a los valores más pequeños, asignándole el valor 1 (el óptimo) al valor mínimo y 0 al valor máximo del criterio que se esté considerando. Como en este ejemplo se consideraron los valores máximos y mínimos de las alternativas a evaluar, al valor 0,5 de K le corresponderá el 1, al igual que al 0 del CII.
En el caso del criterio K la función tiene la siguiente ecuación f(x)=( 2,03 - x ) / ( 2,03 - 0,5 ).
De forma similar, para el caso del criterio CII, la función resulta ser f(x)=(2465,04-x) / (2465,04-0).
Por consiguiente, la matriz con valores normalizados resulta ser la siguiente:
Etapa 5:
Se consulta al usuario acerca de la importancia relativa de cada uno de los criterios y se construye la función de preferencia. Sea α el peso del criterio “K” y β el peso del criterio “Costo de inversión inicial” (CII). De esta manera resulta que:
α+β=1, luego β=1-α
Los valores de α y β se pueden obtener a partir de métodos como: consulta a expertos, el método Delphi o el uso de AHP (proceso de análisis jerárquico). En el trabajo de Hill et al. (2005), por citar un ejemplo, se utilizó AHP.
En consecuencia, la función de preferencia tendrá la siguiente forma:
f (K , CII) = α K + β CII
Etapa 6:
En esta etapa se aplica a cada vector de la matriz con valores normalizados, la función de preferencia para obtener una puntuación. En este punto, se continúa el ejercicio suponiendo que ambos criterios tengan igual importancia (0,5).
Caso α=β=0,5
alternativa 0=f (0,1) =0,5 x 0+0,5 x 1=0,5
alternativa 1=f (0,928,0,611) =0,5 x 0,928+0,5 x 0,611=0,7695
alternativa 2=f (1,0) =0,5 x 1+0,5 x 0=0,5
Etapa 7:
Vistos los resultados de la etapa anterior, se observa que la alternativa 1 tiene el mayor puntaje y, por lo tanto, es la mejor (considerando que el peso de ambos criterios es el mismo en este caso).
Mejor alternativa = alternativa 1.
Aquí finaliza la aplicación de la metodología suponiendo que ambos criterios tienen igual importancia.
A continuación, se presenta un análisis más detallado donde se analizan las mejores alternativas para los diferentes valores posibles de α (y consecuentemente β = 1 - α). Es decir, se procederá a analizar lo que ocurriría para distintos valores de α y β pues 0 <= α, β <= 1 y además α + β = 1.
Sean:
KAlt0 =0 (K normalizado de la alternativa 0 -caso base-)
CIIAlt0 =1 (Costo de inversión inicial normalizado de la alternativa 0)
KAlt1 =0,928 (K normalizado de la alternativa 1)
CIIAlt1 =0,611 (Costo de inversión inicial normalizado de la alternativa 1)
KAlt2 =1 (K normalizado de la alternativa 2)
CIIAlt2 =0 (Costo de inversión inicial normalizado de la alternativa 2)
Una vez analizadas las mejores alternativas para los diferentes valores, el siguiente paso consiste en buscar, para cada par posible de alternativas, valores de α en que el par de alternativas alcancen el mismo valor en la función de preferencia.
Caso 1: Alternativa 0 = Alternativa 1
α KAlt0 + (1-α) CIIAlt0=α KAlt1 + (1-α) CIIAlt1
α 0 + (1-α) 1=α 0,928 + (1-α) 0,611
Despejando α de la igualdad, se obtiene que α = 0,295. Por lo tanto:
Para α<0,295 la alternativa 0 (caso base) es mejor que la alternativa 1.
Para α>0,295 la alternativa 1 es mejor que la alternativa 0.
Para α=0,295 las alternativas 0 y 1 son igualmente buenas.
Caso 2: Alternativa 0 = Alternativa 2
α KAlt0 + (1-α) CIIAlt0=α KAlt2 + (1-α) CIIAlt2
α 0 + (1-α) 1=α 1 + (1-α) 0
Despejando α de la igualdad, se obtiene que α = 0,5. Por lo tanto:
Para α<0,5 la alternativa 0 es mejor que la alternativa 2.
Para α=0,5 la alternativa 0 (situación base) es igual a la alternativa 2.
Para α>0,5 la alternativa 2 es mejor que la alternativa 0 (situación base).
Caso 3: Alternativa 1 = Alternativa 2
α KAlt1 + (1-α) CIIAlt1=α KAlt2 + (1-α) CIIAlt2
α 0,928 + (1-α) 0,611=α 1 + (1-α) 0
Despejando α de la igualdad, se obtiene que α = 0,895. Por lo tanto:
Para α<0,895 la alternativa 1 es mejor que la alternativa 2.
Para α=0,895 las alternativas 1 y 2 son igualmente buenas.
Para α>0,895 la alternativa 2 es mejor que la alternativa 1.
A partir de los resultados anteriores es posible determinar la mejor alternativa para cualquier valor de α en el intervalo (0,1) (Figura 2).
Los resultados obtenidos son los siguientes:
Para 0<α<0,295 la mejor alternativa es la 0.
Para α=0,295 la alternativa 0 y la 1 son (ambas) soluciones óptimas.
Para 0,295<α<0,895 la mejor alternativa es la 1.
Para α=0,895 la alternativa 1 y la 2 son (ambas) soluciones óptimas.
Para α>0,895 la mejor alternativa es la alternativa 2.
Para 0,295<α<0,895 la mejor alternativa es la 1. Obsérvese que esto confirma que esta alternativa es la mejor cuando α vale 0,5 como se demostró al aplicar la metodología asumiendo que los criterios tenían igual peso.

Figura 4: Gráfico que señala la alternativa tecnológica-constructiva que se debe implementar, en función de los posibles valores de α.
Fuente: Elaboración propia.
Así, como puede observarse en la figura 4, es posible determinar la mejor solución tecnológica-constructiva cualquiera sea el peso asignado a cada criterio.
Conclusiones
La metodología desarrollada permitió determinar la mejor alternativa tecnológica-constructiva para la mejora de la eficiencia energética (de la envolvente edilicia en este caso) cualquiera sea el peso o importancia relativa de los criterios considerados. En el caso de que se deseen evaluar diferentes estrategias de energías renovables, debe reemplazarse el criterio relacionado a la eficiencia energética por, por ejemplo, emisiones de CO2 equivalentes evitadas o costo de energía primaria, pues reemplazar energía fósil por renovable no implica un ahorro de energía sino una reducción de emisiones y mayor beneficio en términos ambientales. Así, debería calcularse el aporte suministrado por las energías renovables y calcularse las emisiones evitadas correspondientes si las fuentes de energía fuesen de origen fósil. Esto supone, además, un ahorro de presupuesto por sustitución del tipo de energía, ya que el servicio de gas o electricidad por red (fuentes tradicionales) y sus respectivos costos se reemplazan por energías renovables.
La metodología planteada permitió decidir y fundamentar la adopción de alternativas tecnológicas/constructivas para la mejora de la eficiencia energética (de la envolvente edilicia en este caso) La misma puede ser aplicada en sectores diferentes al de salud como lo son el residencial, educación, comercial, o industrial, entre otros.
Así, la metodología expuesta sirve de apoyo a la toma de decisiones en la elección de alternativas que intenten mejorar la eficiencia energética edilicia y/o incorporar energías renovables. Dichas mejoras contribuirán a que se mejore el nivel de habitabilidad y a que se reduzcan los impactos ambientales en términos de emisones de CO2, entre otros beneficios. Además, es posible incorporar la opinión de usuarios y expertos en la toma de decisiones (en la función de preferencia) generando, de esta forma, alternativas que adoptan un enfoque participativo.
En síntesis, la evaluación multicriterio y el desarrollo de modelos instrumentales constituyen herramientas metodológicas útiles en los procesos de evaluación y planificación energética.

















