The Hospital Anxiety and Depression Scale (HADS) is an instrument for screening symptoms of anxiety and depression that is widely applied internationally, having been adapted to more than 15 languages (Cosco, Doyle, Ward & McGee, 2012), including Brazilian Portuguese (Botega, Bio, Zomignani, Garcia Júnior & Pereira, 1995). The HADS was developed for use in general medical outpatient clinics, although it is widely used in clinical research and practice (Crawford, Henry, Crombie & Taylor, 2001). Thus, the scale is more sensitive to mild forms of psychiatric disorders, avoiding the “floor effect” commonly observed when questionnaires developed to clinical populations are applied in non-clinical populations (Herrmann, 1997). Several studies have indicated its applicability to clinical and non-clinical populations (see Bjelland, Dahl, Haug & Neckelmann, 2002; Westhoff-Bleck et al., 2019). Furthermore, the HADS is considered to be practical (14 items, 7 for each disorder), easy to apply (can be self-administered) and simple to interpret, because it has a cutoff point regarding the presence of significant symptomology for possible or probable cases of each disorder (Faro, 2015).
Examination of the psychometric properties of the HADS, through confirmatory factor analysis (CFA), has been performed internationally since at least 2000 (Bjelland et al., 2002). The first study conducted in Brazil was published in 2015 (Faro, 2015). The studies testing the factorial structure of the HADS through CFA have addressed the adequacy of the original model (bifactorial) in comparison with alternative factorial structures, especially using samples of adults in clinical or non-clinical conditions (see Bjelland et al., 2002; Cosco et al., 2012). In contrast, studies testing the factorial structure of the HADS in samples of adolescents are scarce: to the best of our knowledge, only two have been published so far (Chan, Leung, Fong, Leung & Lee, 2010; Mihalca & Pilecka, 2015). In face of the high prevalence of common mental disorders among Brazilian adolescents, which is approximately 38 % in girls and 22 % in boys (Lopes et al., 2016), evaluate the psychometric parameters of HADS in a sample of adolescents is justified given its usefulness as a screening tool (Chan et al., 2010). Since the common mental disorders’ symptoms are often vague, making these disorders poorly identified by school administrators or even health services (Lopes et al., 2016), a brief and reliable screening tool, like HADS, can be useful in the early identification of these symptoms, favoring further evaluation and assistance.
Furthermore, a gap exists in the literature (even involving adults) investigating whether the bifactorial structure of the HADS is gender invariant (see Cosco et al., 2012), although there is evidence that the symptoms of anxiety and depression can be different in men and women (Cavanagh, Wilson, Kavanagh & Caputi, 2017; Hammen, 2018; Salk, 2017). The literature shows that adolescence is a critical period for the development of these disorders, and that differences exist in some clinical symptomatic manifestations, at the start and during the progression of the disorders with respect to gender, specifically in this age range (Bulhões, Ramos, Severo, Dias & Barros, 2019; Fredrick, Demaray, Malecki & Dorio, 2018; Krause et al., 2017).
Finally, given the shortage of works and the relevance of a deeper understanding of the structure of the HADS in different groups, we tested the bifactorial structure (anxiety and depression) of the HADS and evaluated whether that structure is invariant in function of the gender in a non-clinical sample of adolescents. We also assessed the composite reliability, common method bias and average variance extracted of the HADS and its respective factors.
Method
Research design
This was an instrumental study, based on a cross-sectional survey with a sample of adolescents.
Participants
The sample was composed of 657 high school students from two Brazilian states, 69.9 % (n = 459) from Sergipe and 30.1 % (n = 198) from Paraiba. The majority were girls (58.3 %; n = 383) and the average age was 16.3 years (SD= 1.19), while 74.3 % (n = 488) of the participants were from public schools and the rest from private ones. The grade distribution was 38.1 % in the 10th grade (n = 250), 36.5 % in the 11th (n = 243) and 25.4 % (n = 167) in the 12th. There were no significant differences as to sex and age between the two states (p≥ .05). Proportionally, there were only significantly more participants in the 11th grade in the sample from Sergipe (42.7 %, n = 196) than the sample from Paraíba (22.2 %, n = 44) (χ²= 25.044; p< .001). The other grade strata were proportionally similar.
Procedure
This study was approved by the research ethics committee of the Federal University of Sergipe (registration number 1.505.545). The sample was chosen by convenience, and the data were collected in the classroom after approval by the respective school administrators and parents or formal caregivers through an informed consent. Teachers were present when the students filled out the instrument. All the adolescents first signed the informed agreement form in two counterparts.
Instruments
The HADS contains 14 sentences in two sub-scales: HADS-A (Anxiety, odd-numbered items) and HADS-D (Depression, even-numbered items). The cutoff point of ≥ 9 is considered the most common in studies using the HADS (Cosco et al., 2012; Faro, 2015). It was applied the Brazilian version of the HADS, translated, adapted, and validated by Botega et al. (1995). The diagnostic classification provided by the HADS refers to the screening of significant symptoms of the mild anxiety disorder (MAD) and mild depressive disorder (MDD). The responses are on a scale from 0 to 3 points for each item, so that the highest possible sum for each sub-scale is 21. Finally, sociodemographic data are collected, such as gender, age and school grade.
Data analysis
For descriptive reasons, we calculated the mean and standard deviation of the items in the total sample and by gender. It was also estimated the inter-item and item-total correlations, the mean of the explained variance of the items, and the Cronbach’s Alpha (α) for the internal consistence of the HADS, HADS-A and HADS-D.
Confirmatory Factor Analysis (CFA) was performed by the maximum likelihood estimation method (AMOS, version 22). There were four measures of adjustment of the models: (i) chi-square to degrees of freedom ratio (χ²/df, desirable < 3); (ii) Goodness of Fit Index (GFI, desirable > .95); (iii) Comparative Fit Index (CFI, desirable > .95); and (iv) Root Mean Square Error of Approximation (RMSEA, desirable < .06 and p-close > .500; Marôco, 2014). The gender invariance was analyzed based on two steps: the configural invariance (unconstrained model) and the metric invariance (measurement weights). The parameters applied to reject invariance were ΔCFI (≥ .01) and ΔRMSEA (≥ .015), which reveal the volume of discrepancy of the model fit without and with invariance constraints (Marôco, 2014).
We applied the Common Method Bias (CMB) test, in which the expectation is that the standardized regression weights of the model with one Common Latent Factor (CLF) is not greater than .200 in relation to the model without a CLF (Podsakoff, MacKenzie & Podsakoff, 2012). Finally, we calculated the composite reliability (CR, desirable > .70) and average variance extracted (AVE, desirable > .50) to assess the reliability and precision of the measure, respectively (Marôco, 2014; Valentini & Damásio, 2016).
Results
The descriptive statistics of the HADS items are detailed in the Table 1. The items with the highest and lowest means in the scale were: items 3 (1.4) and 4 (.4) in the total sample; items 5 (1.3) and 4 (.4) for males; and items 8 (1.7) and 4 (.4) for females. Any negative values were found in the subscales or the total scale inter-items indices. The inter-item correlations varied from .20 (items 7-11) to .51 (items 9-13) in the HADS-A, from .11 (items 2-10) to .48 (items 4-6) in the HADS-D, and from .04 (items 2-5) to .51 (items 9-13) in the HADS. The mean of the inter-item correlations was: HADS-A, .38 (.078); HADS-D, .25 (.103); and HADS, .28 (.111). The mean of the item-total correlations was .48 (.118). The total explained variance showed a mean of .31 (31 %), with the following Cronbach’s Alpha coefficients: HADS-A, .81; HADS-D, .69; and HADS, .84.
Table 1: Descriptive statistics of the HADS in the total sample and by gender
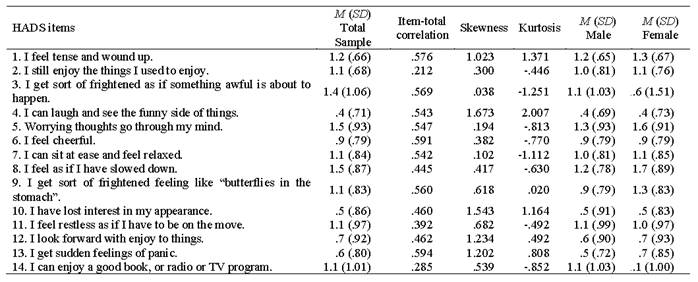
Note: 1. M = Mean 2. SD = Standard Deviation.
The CFA was performed with the two correlated latent factors (HADS-A and HADS-D), and a desirable fit was achieved after inclusion of 5 covariances between the measurement errors, based on inspection of the modification indices. In the HADS-A, the errors of the following items were correlated: 3 and 9 (.22), and 9 and 13 (.16), while in the HADS-D, items 12 and 14 (.17), 6 and 8 (-.28), and 4 and 8 (-.23) were correlated. The correlation between the factors was .83. The value of χ²/df was 2.3, with GFI of .965, CFI of .960 and RMSEA (90 % CI) of .045 (.036 - .054, p-close= .830). Table 2 reports the regression weights and correlations between the factors in the full sample and by gender.
Table 2: Standard regression weights (factor loadings) and correlation indices of the HADS model in the total sample and by gender

Note: 1. Anx = HADS-A (Anxiety); Dep = HADS-D (Depression). 2. Factor loadings after bootstrapping (2000 simulations, all significant in p < .005).
Then we tested the model’s gender invariance. First we detected configural invariance, i.e., the structure of the HADS with free parameters was equivalent in both groups (χ²/df = 1.6; GFI= .952; CFI = .960; RMSEA (90 % CI) = .031 (.024 - .038 and p-close = 1.000)), with ΔCFI below .001 and ΔRMSEA of .014, both within the desirable limit. That finding was corroborated because although the highest discrepancies by gender were observed for items 9 (z = -1.491) and 1 (z = -1.467) in the HADS-A, and for items 8 (z = -1.204) and 6 (z = -1.110) in the HADS-D, the regression weights of all 14 items did not differ significantly for males and females.
Regarding the metric invariance, the difference between the values of χ² in the comparison between the models with unconstrained parameters (232.352, df = 142) and fully constrained parameters (253.291, df= 156) was not significant (χ²(df)= 20.939 (14), p = .103), revealing that the model was invariant to the regression weights in function of gender ( χ²/df = 1,6, GFI= .948, CFI = .956, RMSEA (90 % CI) = .031 (.024 - .038) and p-close = 1.000). Finally, the values of ΔCFI (.004) and ΔRMSEA (< .001) were below the thresholds for rejection of invariance, demonstrating the metric equivalence of the HADS in function of gender.
The analysis of CMB revealed no differences greater than .200 between the standardized regression weights with and without a common latent factor. The CR calculation showed that both factors had desirable values (HADS-A, CR = .80 and HADS-D, CR = .71). Finally, the AVE values of the HADS-A and HADS-D were .37 and .28, respectively, below the desirable cutoff point (> .50).
Discussion
The results of this study provide evidence of the validity of the structure of the HADS in a sample of adolescents, in accordance with results obtained with adult test subjects (Faro, 2015; Lin & Pakpour, 2017; Nezlek, Rusanowska, Holas & Kreptz, 2019; Roberts, Fletcher & Merrick, 2014) and adolescents (Chan et al., 2010). We detected a good fit of the bifactorial HADS model with the inclusion of five cross-loadings between items. The inclusion of the covariance between the errors is not contraindicated when this occurs within the latent factors themselves, because it reflects the existence of a relationship between the characteristics of the items (Marôco, 2014). Since the HADS is a measure for screening symptoms of anxiety and depression, the cross-loadings point to the expected co-occurrence of characteristics of the clinical situations (Eysenck & Fajkowska, 2017), making it plausible, under justifiable conditions, to associate measurement errors. In any event, as pointed out by Nezlek et al. (2019), this type of modification of the model implies a certain limitation on its replicability for similar samples in other populations.
Among the indicators of the CFA of the HADS, the factor loading values of some items stood out. To support the model’s validity, items should have regression weights of at least .60 or .70, depending on the author considered (Marôco, 2014). In the HADS-A, the average factor loading was .61 (SD = .078) while in the HADS-D it was .51 (SD = .173), below the recommended value. Average values of ≥ .50 and ≤ .70 were also found in similar studies, also having good fits in the CFA of the HADS (Annunziata, Muzzatti & Altoè, 2011, HADS-A = .70 and HADS-D = .65; Lin & Pakpour, 2017, HADS-A = .66 and HADS-D = .60; Roberts et al., 2014, HADS-A= .66 and HADS-D = .51). Another study with adolescents found a basically equal mean value for the HADS-A and a lower value than found here for the HADS-D (Chan et al., 2010; HADS-A = .62 and HADS-D = .45). Therefore, mean factor loadings between .50 and .60 are common when analyzing the HADS, despite the favorable fits in the CFA with different samples.
We found that the HADS model was invariant in function of gender in its structure (number and configuration of factors) and metric (equivalence of factor loadings between groups). That finding shows that the scale has similar qualities for application in both groups, and also allows comparison of the results (Marôco, 2014). Additionally, our results did not find significant presence of CMB, which supports the credibility of the instrument. This aspect gains more importance in this study because analysis of bias was not performed in other CFA studies of the HADS (e.g., Annunziata et al., 2011; Roberts et al., 2014), even the most recent ones (e.g., Lin & Pakpour, 2017; Stott et al., 2017).
The findings on the CMB did not show any relevant differences in relation to the standardized regression weights. Thus, these indicators were not substantially influenced by questions related to, for instance, social desirability, cross-sectional design, or adverse effects of the composition of the items, which would have favored a false common variance of the method (Podsakoff et al., 2012).
The CR had satisfactory values, especially in the case of the HADS-A. A high CR is an indicator of internal consistency of the relationship of the items in the factor and suggests the reliable reproducibility of the measure in similar samples. Some studies of the HADS applying CFA have assessed the CR in their samples (e.g., Haugan & Drageset, 2014), but in general, studies have only applied Cronbach’s alpha (e.g., Roberts et al., 2014), while some have not calculated a reliability measure (e.g., Annunziata et al., 2011; Stott et al., 2017). According to Valentini and Damásio (2016), the CR is more appropriate than Cronbach’s alpha when performing CFA. For that reason, we believe the findings of this investigation shed new light on the validity of the HADS.
Unlike the CR, the AVE was below the desirable limit, especially in the HADS-D. Usually, the AVE is argued to be an indicator of convergent validity in CFA (Fornell & Larcker, 1981). Valentini and Damásio (2016), through a simulation study, showed that the AVE tends to decline with rising homogeneity of the regression weights, while it is also affected by the number of items (the lower the number, the greater the demand for high values to reach the desirable AVE). Therefore, considering the findings of those authors, the average of the factor loadings of the HADS had low standard deviations (< .30, see Valentini & Damásio, 2016), suggesting the loadings were predominantly heterogeneous. Besides this, in the HADS the factors are composed of only a few items (7 each), which also might have caused overestimation of the problem of low regression weights (averages of .61 and .51 for the HADS-A and HADS-D). These two aspects possibly help explain the AVE value in this investigation.
It should be noted that the AVE is also considered to be a very restrictive evaluation index, so that it does not always suitably reflect the quality of the model, meaning it might be possible to judge the reliability just by means of the CR (Malhotra, 2011). Furthermore, it is more appropriate to consider the AVE as a measure of precision rather than of convergent validity, since the AVE involves the average variance that is explained by the latent variable and does not presuppose an external measure for convergence (Valentini & Damásio, 2016). Therefore, since we obtained desirable CR values of the HADS-A and HADS-D, we believe the low AVE value does not undermine the validity of the measure. It can be considered reliable (satisfactory CR), although a caveat is warranted regarding the precision of the measure (low AVE).
The problem detected here with the low AVE and factor loadings is something that should be analyzed in future studies. For that purpose, a suggested strategy is to remove the items with the lowest factor loadings (Malhotra, 2011). In this sample, items 2, 11 and 14 had the lowest regression weights, making them possible targets for deletion from the model. However, we decided not to alter the scale’s factorial structure, since except for the AVE, the findings were satisfactory, including the model’s invariance. Besides this, since our sample consisted only of adolescents from two Brazilian states, we believe these findings, although important, do not (yet) provide sufficient indications that the HADS would produce different results with this public in other contexts, which would justify possible removal of items and change in the measure’s structure.
The choice to maintain the model also was based on the fact it has been found to be a good solution with the basic structure of two factors and seven items per factor, since the scale has shown good clinical utility in its original format (Bjelland et al., 2002; Cosco et al., 2012; Roberts et al., 2014). This is a debate similar to that raised in a recent study in Sweden (Djukanovic, Carlsson & Arestedt, 2017). Furthermore, the reduction of the number of items would affect the cutoff point of the scale, since it is a diagnostic screening instrument. Consequently, a validity study would be necessary for redefinition of its classification rule, which was not the objective of this investigation. Comments in a similar direction were made in a study of adults suffering from dementia (Stott et al., 2017). In summary, particularly because our sample consisted of adolescents, there is a need for more evidence of the psychometric qualities of the HADS for this group, especially regarding the aspects detected.
Further studies of the theme are warranted, since more psychometric evaluations of the HADS in Brazil, to the effect of psychological interventions related to depressive and anxious disorders in adolescents. A specific suggestion is related to performing a CFA with a clinical sample of adolescents in order to verify the structural equivalence between different sample profiles. A last recommendation is a population screening of depressive and anxious symptomatology in Brazilian adolescents, because the extension of the HADS makes it possible to reach a wide public through a free and brief instrument, which significantly reduces research costs.
The main limitation of this study was that it did not involve analysis of criterion validity, so the results found apply to the HADS in its original format and not to diagnostic categorization. Additionally, these findings do not include other questions that are also pertinent to psychometric evaluation, such as the quality of the items, which can be addressed by item response theory and/or Rasch analysis, as have been applied in recent works (e.g., Ayis, Ayerbe, Ashworth & Wolfe, 2018; Lin & Pakpour, 2017; Lin et al., 2017; LoMartire, Ang, Gerdle, & Vixner, 2019).
Finally, the main contribution of this study is the confirmation of the structure and invariance of the HADS among adolescents, which corroborates the instrument’s validity, as well as the possibility of comparison between the genders. The results show some positive aspects regarding the use of the HADS, but also some fragilities, reflecting the continuous and dynamic construction of scientific knowledge.















