Introducción

Cuando un ingeniero agrícola estudia una obra hidráulica desde una alcantarilla, un canal de drenaje (como una terraza agrícola) o desde el vertedero de un tajamar o una represa, debe realizar una aproximación de la realidad de una cuenca a través del análisis de las relaciones lluvia-escurrimiento (en base a modelos) y, con el análisis de frecuencias de precipitaciones, convertir la lluvia de diseño en un caudal de diseño. Cualquier modelo o método de determinación de máximos caudales de escorrentía de una cuenca determinada requiere de la determinación del tiempo de concentración de la cuenca. El tiempo de concentración de la cuenca es el tiempo que demora en llegar el agua de escurrimiento que se genera en la parte más alejada de la cuenca hasta el punto de salida en consideración o punto de interés en la cuenca analizada. Los modelos de caudales de escorrentía más corrientes en la ingeniería agrícola son la ecuación racional¹ y el modelo TR-55².

El modelo TR-55 es un modelo hidrológico que transforma la precipitación (P) máxima en 24 horas caída en una cuenca, con sus diferentes suelos, usos y manejo de los mismos, en un caudal (Q) de salida en un punto de la vía de drenaje principal de la cuenca. El modelo está basado en el concepto del número de curva (CN) y la clasificación hidrológica de los suelos de la cuenca, para de-terminar el valor de escorrentía que se genera en ocasión de lluvias. Como el modelo es importante para la determinación de caudales extremos que ocurren en ocasión de lluvias extremas, tiene como función clave introducir el valor más correcto de P (mm) en 24 horas para que, conjuntamente con el tiempo de concentración de la cuenca (tc) y el CN, sea posible generar el dato de escorrentía Q en altura (mm) y también el máximo caudal Q (m³/s). Además de la determinación del caudal máximo, el modelo permite transitar la creciente de diseño, a través de la estructura hidráulica, determinando el efecto de la misma en la cuenca. El tránsito del hidrograma de la creciente a través del lugar donde se construirá la estructura, permite analizar cuantitativamente el efecto de dicha estructura en los caudales resultantes aguas abajo de la misma.

Los datos hidrológicos como la precipitación (P) pue-den ser tratados como variables estadísticas, y especial-mente la precipitación puede ser considerada como una variable aleatoria independiente, por ejemplo, en este caso, de máximos anuales en 24 horas, por lo cual podemos ajustar funciones de densidad de probabilidad como la de valores extremos u otra. Es decir, existen varias funciones de densidad de probabilidades, que se pueden utilizar eficazmente para determinar la probabilidad de ocurrencia o el período de retorno (T) de lluvias extremas³.

El período de retorno T es un término común en la ingeniería agrícola y en hidrología para expresar la rareza de un evento de precipitación; cuanto mayor es el período de retorno estamos manejando eventos más extremos y menos probables, ya que el período de retorno es el inverso de la probabilidad de ocurrencia T = 1/P.

El período de retorno T es el número de años en que un evento determinado puede ser igualado o excedido por lo menos una vez⁴. Quiere decir que una precipitación de 145 mm en 24 horas con un T = 20 años, significa que la magnitud puede ser igualada o superada 20 veces en 100 años o, en otros términos, la probabilidad de ocurrencia de la misma (P ≤ 1/5) es igual o menor a 0,20.

Por tanto, se define período de retorno como el número de años³ para que un evento (caudal Q o precipitación P) de cierta magnitud sea igualado o excedido. Esto no implica una periodicidad. Así, un T = 10 años para una lluvia de 120 mm/24 horas, significa que la magnitud será igualada o excedida 10 veces en 100 años, pero no quiere decir que ocurriría a intervalos regulares de 10 años.

La distribución de valores extremos Tipo I⁵, también conocida como método de Gumbel, ha sido ampliamente utilizada en los EEUU⁶ y otras partes del mundo⁷, para determinar períodos de retorno de valores extremos de precipitación y de caudales.

La teoría de los valores extremos fue investigada originalmente por Fisher y Tippett⁵ y aplicada a datos hidrológicos por Gumbel⁸. Dicha teoría establece que una serie de n valores anuales máximos se aproxima o sigue una función de densidad de probabilidad cuan-do tenemos un número de observaciones grande. Esta teoría ha tenido aplicación inmediata siempre en los valores de caudales en ríos y arroyos, pero también en las precipitaciones, cuando estas pueden considerar-se variables independientes, como es el caso de máximos anuales en 24 horas.

Chow⁴ ha demostrado que la mayoría de las funciones de densidad de probabilidad o de frecuencia de las variables de precipitación o de caudales extremos se pue-den generalizar bajo una única y sencilla fórmula de gran utilidad práctica, tomando máximos anuales en 24 horas para una serie de años «n» de una estación pluviométrica:

donde y es el evento con una probabilidad determinada, y_MEDIA es el valor medio de la serie de datos, y σ^y es la desviación estándar de la serie de datos. Los valores yn en nuestro caso son los máximos anuales.

El ajuste de la información de máximos anuales de caudales de un río o de precipitación en una estación meteorológica, puede ajustarse a diferentes funciones de densidad de probabilidad, Gumbel, log-normal, Pearson tipo III. Sin embargo la función más antigua, clásica y aceptada es la de Gumbel⁸, y esta es la que fue utilizada hace 40 años.

El método gráfico de verificación del ajuste de los datos a una determinada distribución de probabilidad es un método clásico práctico, donde los puntos de los valores registrados se grafican sobre un papel en escala semilo-garítmica, donde las abscisas son el período de retorno T (escala logarítmica) y las ordenadas (escala aritmética) los valores de precipitación máxima en 24 horas. Los puntos ubicados en el correspondiente papel de acuerdo a un criterio de ploteo, por ejemplo Weibull, tras lo cual se traza la función de densidad y se determina a ojo el grado de ajuste de los datos a la función de probabilidad.

Para la comprobación de un buen ajuste de información pluviométrica máxima en 24 horas con diferentes probabilidades de ocurrencia, a una determinada función de densidad de probabilidades, es necesario en primer lugar clasificar los datos máximos anuales en orden de-creciente y a cada uno asignarle un número de orden m, donde el total de datos es el número n. La frecuencia con la cual sería igualado o excedido un evento de orden m es de acuerdo con Weibull⁶:

F = m / ( n + 1) ( Método de Weibull)

Hay otros métodos más precisos como la comprobación del ajuste por el método de los mínimos cuadrados, que se analizarán con vistas a investigar el probable efecto de cambio climático.

Actualmente se ha desarrollado el modelo WinTR55⁹, que es un modelo simplificado de procedimientos para estimar escurrimientos y máximas descargas en peque-ñas cuencas (< 6.500 ha), con tiempos de concentración menores a 10 horas, así como hidrogramas en la salida de una cuenca con la posibilidad de hasta 10 subcuencas. El programa no sólo es un avance en el sistema, de pasar del DOS a Windows, sino que supone la introducción de un programa hidrológico más avanzado, el TR20⁹.

Por ello, con vistas a realizar un nueva adaptación del modelo TR-55, ahora en versión Windows, que ya hace varios años que está disponible libremente, y dado que también está disponible una clasificación hidrológica actualizada de los suelos del país¹⁰, el objetivo principal del presente trabajo es la actualización del modelo TR-55 en Uruguay a la versión Windows de la adaptación del WinTR55⁹, para resolver problemas hidrológicos e hidráulicos relacionados con obras de ingeniería agrícola. Para ello es fundamental manejar y procesar información pluviométrica máxima en 24 horas, de acuerdo con una metodología, y obtener valores fidedignos, para diferentes períodos de retorno. Este tipo de información ha sido realizado en EEUU confeccionando cartas para diferentes períodos de re-torno de las precipitaciones máximas desde 30 minutos hasta en 24 horas¹¹, un estudio clásico de referencia. Este trabajo es una actualización de un trabajo presentado por Koolhaas¹², donde fue realizado idéntico estudio pero para el período 1940 a 1970 en 81 estaciones pluviométricas de la Red Básica del Servicio Pluvio-métrico de la Dirección de Meteorología de Uruguay

Materiales y métodos

En este estudio se solicitaron a Inumet (Instituto Uruguayo de Meteorología) los datos de lluvia máxima en 24 horas por año para una serie comprendida entre 1970 y 2010, para las mismas estaciones pluviométricas del estudio previo¹². Sin embargo, el número de estaciones ha disminuido a 56 por razones presupuestales de disminución de personal afectado a la observación meteorológica, incluso en algunos casos sólo fue posible obtener 20 años de información en lugar de 40 años. En efecto, este es el caso para Pan de Azúcar, donde la información proviene de 20 años salteados y Chuy, n = 24 años, entre 1981 y 1996; para el resto, oscila entre 30 y 40 años. La densidad de estaciones tomada determina que en promedio cada estación representa 3.340 km² del Uruguay y, por tanto, considerando áreas circulares, existe una determinación pluviométrica cada 65 km, aproximadamente. La información fue proporcionada en Excel, y el procesamiento de la información fue realizado en el mismo archivo. Para cada una de las estaciones se procedió a obtener la media aritmética, el desvío estándar y el coeficiente de variación, para aplicar la fórmula general de Chow⁴ para el método de Gumbel¹³ o función de densidad de probabilidad para valores extremos.

En la fórmula (1) los valores de K, o factor de frecuencia, son función del período de retorno, la Figura 1 muestra una representación del factor de frecuencia en función del período de retorno T.

Figura 1: Factor de frecuencia K para el método de Gumbel, utilizando la fórmula general de Chow⁴. 

Una vez procesada la información en las planillas Excel¹⁴, se preparó una cartilla con las diferentes estaciones y los diferentes períodos de retorno. Estos datos son los que se cargaran en archivos de texto para el software WinTR55, los cuales estarán todos dentro de una carpeta nominada Uruguay.

Las cartas se obtienen cargando las coordenadas planas en formato Gauss-Kruger con el valor de P₂₄ máxima para cada uno de los períodos de retorno, generándose un archivo de texto con las 51 estaciones pluviométricas georreferenciables a través de coordenadas planas con su valor de precipitación. De esta manera, ese archivo de texto se manejó en el software de generación de curvas de nivel LI Contour¹⁵ para generar las diferentes cartas adjuntas en un CAD¹⁶.

Resultados

Los resultados de este trabajo son las diferentes cartas que se muestran a continuación, donde aparecen arregla-das sobre programa CAD las curvas o isolíneas de igual P_24horas en una carta georreferenciada de Uruguay, en coordenadas planas en el sistema ROU-USAMS (Gauss-Kruger), el mismo sistema cartográfico del Servicio Geo-gráfico Militar del Uruguay utilizado en todas las cartas existentes e impresas del país (Figuras 2, 3, 4, 5, 6 y 7).

Figura 2: Máxima cantidad de lluvia en 24 horas para un T = 2 años. Serie de datos Inumet (Uruguay). Coordenadas Gauss-Kruger (ROU-USAM) en kilómetros. 

Figura 3: Máxima cantidad de lluvia en 24 horas para un T = 5 años. Serie de datos Inumet (Uruguay). Coordenadas Gauss-Kruger (ROU-USAM) en kilómetros. 

Figura 4: Máxima cantidad de lluvia en 24 horas para un T = 10 años. Serie de datos Inumet (Uruguay). Coordenadas Gauss-Kruger (ROU-USAM) en kilómetros. 

Figura 5: Máxima cantidad de lluvia en 24 horas para un T = 25 años. Serie de datos Inumet (Uruguay). Coordenadas Gauss-Kruger (ROUUSAM) en kilómetros. 

Figura 6: Máxima cantidad de lluvia en 24 horas para un T = 50 años. Serie de datos Inumet (Uruguay). Coordenadas Gauss-Kruger (ROU-USAM) en kilómetros. 

Figura 7: Máxima cantidad de lluvia en 24 horas para un T = 100 años. Serie de datos Inumet (Uruguay). Coordenadas Gauss-Kruger (ROU-USAM) en kilómetros. 

Discusión

En este trabajo se asume el ajuste a la distribución Gumbel de los datos, porque la información recabada, serie anual, conforma la hipótesis de la función Gumbel¹¹, y el objetivo principal está orientado a la práctica profesional de ingeniería agrícola.

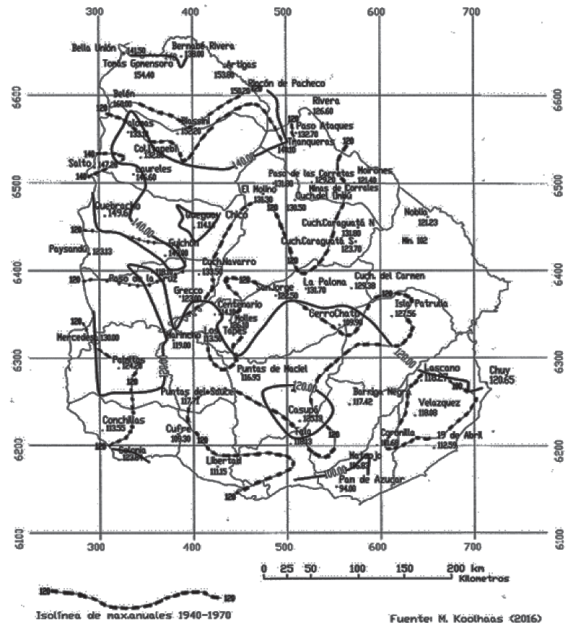
Sin embargo, fueron analizadas las cartas nuevas con las anteriores¹⁷, detectándose para una frecuencia o período de retorno de T = 5 años que hay incrementos en los valores hacia el Litoral Norte en el orden de +20 mm. En las otras cartas de mayores períodos de retorno la diferencia se incrementa hacia +40 mm y también en la zona central del país (Figura 8). Por lo tanto, en principio podría afirmarse, al considerar diferentes períodos de retorno, que al igual que las precipitaciones anuales, las diferentes estaciones pluviométricas del país muestran un incremento del orden del 10 % en períodos de 20-30 años. Estudios de precipitaciones y su variabilidad han sido realizados por distintos autores en Sudamérica que confirman la tendencia creciente y variabilidad mayor¹⁸⁾⁽¹⁹. Esto también se verifica con los máximos anuales en 24 horas. No hay concordancia en el padrón de las curvas representadas en los dos estudios; no obstante, en la observación detallada de las cartas se puede apreciar un cambio en las precipitaciones máximas con una variante mayor en períodos de retorno mayores.

Figura 8: Comparación de máxima precipitación en 24 horas para un T = 5 años con serie 1940-1970.