1. Introduction

Land use has changed drastically in the last 20 years in South American Pampas¹, a region that covers more than 700000 km² in central-eastern Argentina, southern Brazil, and Uruguay. Following these regional trends, the annual cropped area in Uruguay increased from 400000 to 3.055 million ha, with soybean and wheat as main crops². This increase in cropped area occurred mainly by shifting cropping systems from crop-pasture rotations to continuous annual cropping under no-till³.

Current nutrient management recommendation for spring cereals production in Uruguay⁴ was developed between 1992 and 2001, under dominant crop-pasture rotation composed of a three- or four-year annual cash crop phase alternating with a three- or four-year grass-legume pasture phase.

The schedule proposed has three steps: i) amount of N fertilizer at seeding date is defined according to nitrate concentration (N-NO₃ ^-) availability in the top 20 cm of soil; ii) additional N fertilizer is added if N-NO₃ ^- in the 0-20 cm layer is less than 12 mg kg^-1 when wheat is at GS 2.2 stage in the Zadoks scale⁵; and iii) additional N fertilizer is defined at GS 3.0 stage depending if plant N concentration is lower than 42 g kg^-1. Under such conditions, the amount of N fertilizer required is adjusted following a family of response curves to produce maximum grain yields estimated for each field⁶.

When crop-pasture rotation is converted to continuous annual cropping both soil nitrogen (N) supply capacity and N fertilizer use efficiency are reduced⁷, implying increased N fertilizer requirements⁸. This N supply deficit can be diagnosed following current “best management practices”. However, plant N concentration at GS 3.0 and fertilizer rates applied under such guide remain as the yield limiting factor⁷⁾⁽⁹⁾ generating a yield gap (Yg) attributed to N deficit. To close this Yg (difference between attainable yield and actual yield), N fertilization amount at GS 3.0 has being arbitrarily increased⁹, emerging potential negative environmental impacts from N overuse.

Two processes would explain increased N requirements: i) depressed N soil supply¹⁰, and ii) increased N demand because of increased yield potential of the new wheat varieties^11-12.

To promote precise N fertilization management, including amount and timing, the new tools must be based on accurate crop nitrogen requirement estimations. Additionally, N fertilization strategies must be adjusted balancing the often-contradictory goals of maximize production with low negative environmental impacts. Thus, splitting N fertilizer application following crop N requirements throughout the growing season is probably the best strategy. Delaying part of the N fertilizer to the onset of stem elongation usually results in maximum N use efficiency^13-15. However, N required is not a fixed amount split over time, it is a variable amount depending on N supply from the soil and N demand from crop balance. Therefore, reliable indicators of crop N status are required to improve detection and correction of N deficiencies, but avoiding N overfertilization.

Following Lemaire and others¹⁶, the impact of N deficit on wheat grain yield can be quantified applying the concept of critical N concentration (Nc) to diagnose the N status of crops. The value of Nc represents the minimum N concentration that is required for maximum biomass production at different development stages. The concept of a Nc dilution curve based on plant N concentration (% N) was developed by Lemaire and Salette¹⁷, being represented by an algometric function:

Nc = a*DM^−b

where DM is the shoot dry matter expressed in Mg ha⁻¹; Nc is the critical N concentration in shoots expressed in % DM, and a and b are estimated parameters. The parameter a represents the Nc in the shoot DM for 1 Mg ha⁻¹, and the parameter b represents the coefficient of dilution describing the relationship between % N and shoot DM¹⁸.

Under other limiting yield factors than N, this allometric model expresses the N dilution curve (NDC) as the crop cycle progresses¹⁹. Relating % N and crop growth rate might diagnose the nitrogen nutritional status at different phenological stages²⁰. Nitrogen nutrition index (NNI) has been proposed as an indicator to quantify the crop nutritional status related to Nc to non-limited growth (NNI=% N/Nc)¹⁶⁾⁽²¹. The Nc value is derived from NDC.

Although NDC and NNI are known concepts, its use as a diagnoses and prognoses criterion requires to answer at least the following question: at each phenological stage, what is the Nc that does not limit growth rate until the next phenological stage? Being GS 3.3 the last wheat phenological stage to apply N fertilizer maximizing grain yield and N fertilizer use efficiency^13-15, can we use NNI at GS 3.3 to diagnose and predict N deficit and N fertilizer requirement?

Our hypothesis are: i) following current “best management practices”, N supply after GS 3.0 is the wheat yield limiting factor; ii) additional N fertilizer required for wheat production in Uruguay can be adjusted matching the current N recommendations guide⁴ with the NNI at GS 3.3.

The objectives were: i) to determine optimal N status at different phenological stages adjusting the N dilution curve for spring wheat under rainfed conditions; ii) to quantify the wheat yield gap explained by N supply deficit at GS 3.3, and iii) to propose a critical NNI level as predictor of response to N fertilizer applied at GS 3.3.

2. Materials and methods

2.2 Data analysis

Adjusting NDC

We followed the classical approach to determine the NDC¹⁹. N-limiting growth is defined as a treatment in which any additional N application would lead to a significant increase in shoot DM. A non-N-limiting growth treatment is defined as an N application rate that would not lead to an increase in shoot DM but would result in a significant increase in % N. For each phenological stage, the minimum % N necessary to achieve maximum shoot DM is defined as the critical shoot concentration (Nc)¹⁷⁾⁽¹⁹.

DM differences were stablished comparing accumulated DM across the different N treatments by analysis of variance using Infostat. Differences among treatments were defined at p-value≤0.1 level.

The Nc was estimated as follows:

i) For each phenological stage, the variation % N versus shoot DM across different N levels was combined into a bilinear relation composed of (a) a linear regression representing the joint increase in % N and DM, and (b) a vertical line corresponding to an increase in % N without significant variation in shoot DM.

ii) Maximum DM corresponds to the average of the observed data under non-limiting N conditions.

iii) The theoretical Nc corresponds to the breakpoint of these bilinear regressions.

NDC was estimated using an allometric equation fitted to this N critical points, proposed by Lemaire and Salette¹⁷.

Estimating N deficiency at GS 3.3 to maximize grain yield

Two concepts were applied to diagnose the N non-limited/limited growth conditions to maximize wheat yield: NNI¹⁶⁾⁽²¹ and Yg attributed to N^23-24, as follows:

i) We define GS 3.3 as the last phenological stage where grain yield responds to N fertilizer²⁵.

ii) Critical NNI level at GS 3.3 (NNI_critical) was estimated by non-linear regression (two sections with plateau) relating relative yield (RY) and NNI.

NNI corresponds to the ratio between % N of the crop to be diagnosed with the Nc estimated from the NDC (NNI = % N/Nc).

If NNI = 1, N nutrition is considered optimal; if NNI was >1, N nutrition is considered excessive; and if NNI was <1, N nutrition is considered insufficient.

RY= Y/Y_max

where Y= grain yield obtained under a given N rate; Y_max= highest grain yield among all N application rates.

iii) Using data from GS 3.3 only, an NDC at GS 3.3 to maximize grain yield (NDC_yield) resulted from NDC*NNI_critical value. This NDC corresponds to optimum % N at GS 3.3 considering the DM produced until GS 3.3.

Predicting wheat yield response to N applied at GS 3.3

The proposed critical NNI at GS 3.3 as predictor of wheat yield response to N applied at GS 3.3 was evaluated on data from 6 independent experiments (Supplementary material 2). We estimated the NNI from treatments under N=0 at GS 3.3, and grain yield response to N applied at GS 3.3 (N=0 vs N>0), comparing the RY difference between these two N rates.

The conditions of the successes were defined by:

1) NNI ≤ NNI_(RY=1) and RY ≤ 1

2) NNI ≥ 1 and RY ≥ RY_(plateau)

The conditions of error in the diagnosis were divided into two types and were defined by:

1) Type I error. NNI > 1 and RY > 1

2) Type II error. NNI > NNI_(RY=1) and RY < RY_(plateau)

Identifying variables determining yield gap attributed to nitrogen deficiency at GS 3.3

Yield gap (kg ha^-1) attributed to N supply deficit at GS 3.3 was calculated as the difference between yield obtained at each N rate and the highest grain yield obtained without N fertilizer applied at GS 3.3 (Yg=Y_highest-Y).

We used classification and regression tree²⁶ (JMP 8 statistical package) to uncover relationships and interactions between Yg and a suite of crop growth and crop nutrition at GS 3.3. Classification and regression tree is a nonparametric modeling approach that can explain the responses of a dependent variable (Yg) from a set of independent continuous variables or categorical variables, identifying homogeneous subsets based on independent variable. Independent variables included: i) wheat yield obtained under N=0 estimating soil N supply capacity (Y_N=0); ii) attainable wheat yield (Y_max) under no limited by N conditions, but under rainfall conditions -maximum yield (Mg ha^-1) obtained under the best N treatment in each experiment-; iii) crop growth -DM at GS 3.3 (Mg ha^-1), maximum dry matter produced (Mg ha^-1) at GS 6.5 (DM_max) under the best treatment in each experiment-, and iv) crop nutrition estimators (N uptake, NNI, Nc, % N).

Estimating yield gap explained by N supply deficit at GS 3.3

The relative yield gap (RYg) corresponds to Yg related to Y_highest reference (RYg=Yg/Y_highest), representing the relative distance from Y to Y_highest, allowing a normalized comparison of Yg among site-year combinations.

Yield loss due to N deficiency at GS 3.3, was quantified by non-linear regression (lineal-plateau) relating RYg and NNI by soil N supply capacity.

Total N supply is composed by soil N supply (N_soil) plus N fertilizer. N_soil was estimated using the grain yield obtained under the control treatment (N fertilizer rate=0) (YN_soil); it was considered as an estimator of the N contribution capacity from soil throughout the crop cycle, and not just in a growth stage. Diagram on Figure 1 presents the work scheme followed.

Figure 1: Simplified model of stages and processes in research 

3. Results

3.1 Description of the database

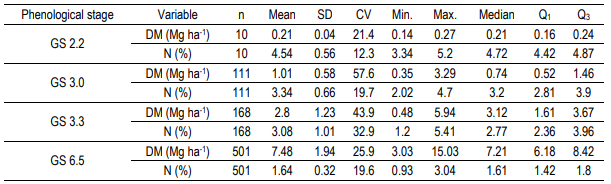
A wide range of DM and % N were obtained at each phenological stage (Table 1). However, data satisfying the statistical requirements described in section 2.2 included shoot DM values between 0.21 and 11.5 Mg ha⁻¹, and % N between 4.5% and 1.2% corresponding to GS 2.2 and GS 6.5, respectively.

Table 1: Descriptive statistics of aerial biomass and total N in plant in GS 2.2, GS 3.0, GS 3.3 and GS 6.5. DM - Aerial biomass (Mg ha^-1). N (%) - N concentration in aerial biomass (%), n - Observations number, SD - Standard deviation, CV - coefficient of variation, Min. - minimum value, Max. - maximum value, Q₁ - Quantile 1, Q₃ - Quantile 3 

3.2 N-dilution curve and critical NNI to GS 3.3

The following function to estimate NDC was adjusted using 37 values of DM, and % N corresponded to growth stages from GS 2.2 to GS 6.5.

Nc = 3.6*DM^-0.31

The model describes the minimum concentration of N needed to obtain the maximum DM production at corresponding phenological stage. It represents the algometric relationship between DM and % N (R² = 0.81; p-value < 0.0001; SE_a = 0.13, and SE_b = 0.03) (Fig. 2a).

The relationship between RY and NNI at GS 3.3 derived from this NDC corresponded to a non-linear model of two sections with plateau (Fig. 2b). The linear phase (R² = 0.74) presented a slope of 0.65 (p-value < 0.0001, SE=0.07) until the NNI_critical value (1.24; p-value < 0.0001, SE = 0.04). Below this NNI_critical the RY increased lineally from 0.13 to 0.94. While NNI ≥ 1.24 indicated that the crop was under non-limiting N conditions, NNI values <1.24 indicated that N was the yield limiting factor.

The NNI_critical value at GS 3.3 discriminate limiting N conditions from non-limiting N conditions to obtain the maximum grain yield.

Figure 3 shows the NDC adjusted using DM variability at GS 3.3 only, and NDC adjusted to maximize grain yield (NDC_yield) (Nc = 4.17*DM^-0.31). The latter has the same N dilution coefficient (b = -0.31), but its Nc is 24% higher than for NDC (a = 3.36 vs a = 4.17, for NDC and NDC_yield, respectively), indicating a greater N requirement to maximize grain yield than to maximize DM at GS 3.3.

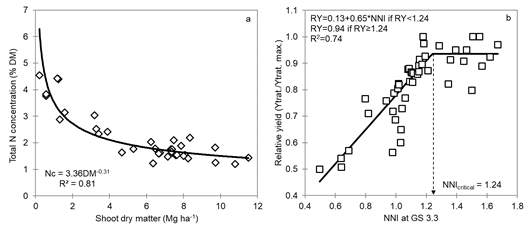
Figure 2: a) Minimum N concentration needed to maximize the production of shoot dry matter for wheat under rainfed conditions. b) Relationship between NNI at GS 3.3 and RY 

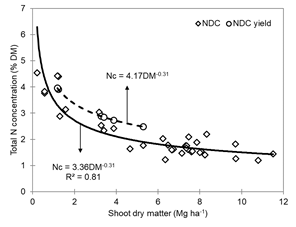
Figure 3: Nitrogen dilution curve for wheat under rainfed conditions. Rhombuses - minimum concentration of % N to maximize crop growth (NDC); Circles - minimum concentration of % N to maximize grain yield (NDC_yield) 

Predicting yield N limiting conditions at GS 3.3

Using NNI at GS 3.3 we can identify 74% of N limiting conditions to maximize grain yield. This performance was improved by 4% using NDC_yield, maintaining both type I error and type II error at 11% (Table 2).

Table 2: Effectiveness of NNIs estimated with NDC and NDC_yield as indicators of N deficiency and response to nitrogen fertilization in GS 3.3 

3.3 Yield gap explained by nitrogen deficiency at GS 3.3

The regression tree model for wheat Yg as a function of soil N supply capacity, attainable wheat yield (Y_max) under no-limited N conditions, crop growth and crop nutrition at GS 3.3 variables is shown in Fig. 4. The overall model explained roughly 59% of Yg variability using the two variables, NNI and YN_soil. The optimum regression tree had 3 splits and 6 terminal groups (TGs). The first split occurred at NNI 0.72. When NNI ≥ 0.72, a new split was produced by NNI = 0.95, which suggested that the N deficiency at GS 3.3 was the most important factor in determining Yg. Inside the two main branches, TGs were defined by YN_soil.

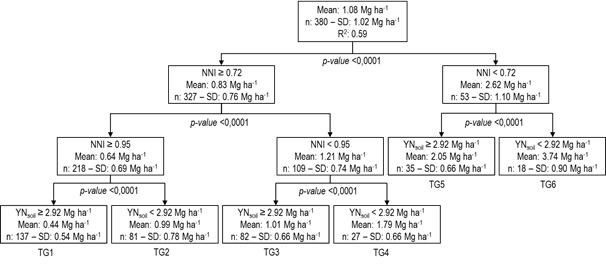
Figure 4: Classification and regression tree describing wheat yield gap (Yg) from nitrogen nutrition index (NNI) at GS 3.3, and yield obtained under soil N supply capacity (YN_soil). Each node (square) is labeled with average Yg (means), standard deviation (SD) and the number (n) of data in that group. The model is read from top down until terminal group (TG) appear. The statistical significances (p-value) are presented at each root node 

While those sites in which YN_soil < 2.92 Mg ha^-1 (TG2, TG4 and TG6) can be classified as low soil N supply capacity (N_soil-Low) (Fig. 4), those that achieved YN_soil ≥ 2.92 Mg ha^-1 (TG1, TG3 and TG5) are considered as high soil N supply capacity (N_soil-High) (Fig. 4). These environments are associated with the N supply capacity by soil, as the N uptake by crop at GS 3.3 (N_uptake) tends to be greater as the yield increases in YN_soil, at a rate of 20 kg N ha^-1 for each Mg ha^-1 of increase in yield (N_uptake = 0.02*YN_soil-14.7, p-value < 0.0001, R² = 0.86). In low-contribution environments, the crop at GS 3.3 absorbed on average 29 kg N ha^-1 with SD 5.9 kg N ha^-1 and CV 20.5%, while in high-contribution environments 55 kg N ha^-1 were absorbed on average with SD 13.8 kg N ha^-1 and CV 25.3%.

We adjust two negative lineal-plateau functions relating RYg to NNI at GS 3.3 (p ≤ 0.05) under N_soil-High and N_soil-Low (Fig. 5a). These functions improved the R² = 0.66 estimated to the average model (RYg = -0.80*NNI+0.88, if NNI < 0.99, p-value < 0.0001, SE = 0.03). The slope (beta 1 coefficient, Fig. 5a) of the decreasing linear phase was -0.97 vs. -0.76; the RYg plateau were 0.03 and 0.10 under N_soil-High and N_soil-Low, respectively, but the thresholds (gamma coefficients, Fig. 5a) were the same (1.04, SE = 0.03, p-value < 0.0001).

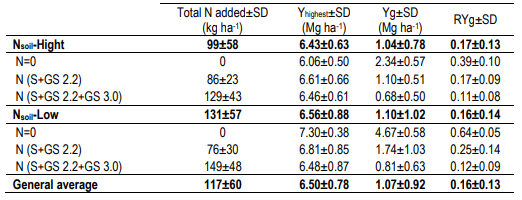
The RYg was higher under N_soil-Low than N_soil-High (0.64 vs 0.39). However, RYg was reduced conforming additional N fertilization included N at seeding date, GS 2.2 and GS 3.0 (N = 0; N = S+GS 2.2; N = S+GS 2.2+GS 3.0) (Fig. 5b). Differences between soil N supply capacity were reflected in total N fertilizer added following the “current best management practices” (Table 3). On average, N added under N_soil-Low was 33% higher than N_soil-High (131 vs 99 kg N ha^-1, p-value = 0.004) (Table 3).

The highest yields (at treatment level in each experiment), used as a reference to calculate the RYg in both soil N supply capacity environments (Table 3), did not differ significantly (p-value: 0.35). Although the average Yg was similar in both environments (1.04 Mg ha^-1 and 1.10 Mg ha^-1 for N_soil-High and N_soil-Low, respectively, p-value: 0.74), the highest Yg was 5.25 Mg ha^-1 in N_soil-Low against 3.04 Mg ha^-1 in N_soil-High (42% difference between environments).

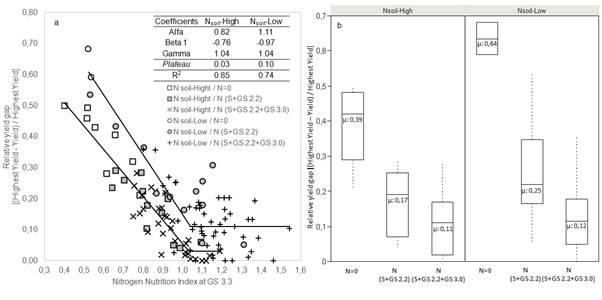
Figure 5: a) Relative yield gap (RYg) caused by nitrogen deficiency to GS 3.3 according to soil N contribution environment. Alfa - intercept, Beta 1 - slope of linear phase, Gamma - NNI value at beginning of plateau (threshold). N=0 - non-N fertilizer, N (S+GS 2.2) - fertilizer at seeding and GS 2.2, N (S+GS 2.2+GS 3.0) - fertilizer at seeding, GS 2.2 and GS 3.0. b) Box plot of RYg by fertilization scheme. Line inside each box indicates median. Whiskers (error bars) above and below box indicate the 90^th and 10^th percentiles. µ - mean 

Table 3: Total N added average, benchmark yield (Y_highest), relative yield gap (RYg) and yield gap (Yg) by environments of soil N supply capacity. N=0 - non-N fertilizer, N (S+GS 2.2) - fertilizer at seeding and GS 2.2, N (S+GS 2.2+GS 3.0) - fertilizer at seeding, GS 2.2 and GS 3.0, SD - standard deviation 

4. Discussion

The NDC for wheat and other crops and pastures is widely reported in the literature for non-limiting water conditions. However, empirical evidence in wheat²⁷ and other crops^28-29 indicates that the nitrogen requirements in cropping systems under rainfed conditions are lower due in part to changes in biomass assignment³⁰. In this work the adjustment was made under the current production conditions for Uruguay, in which the water supply depends on the amount and distribution of rainfall and the ability to store soil water. Under these conditions, the production of DM may be limited by water availability. In our results, biomass production was low, mainly in initial phenological stages (Table 1), being able to limit the attainable yield³⁰ and the recovery efficiency of N³¹. For study conditions, the adjusted NDC_yield has similar coefficients only to those reported by Yue and others³² in northern China and by Greenwood and others³³ in Belgium and Sweden. The difference with the adjusted coefficients in other works results from the expected variation within species¹⁹, experimental sites, phenological stages³³, regions, genotypes and management^34-35, which justifies the need for local adjustment.

Our framework reflects two major changes occurred in cropping systems during the last 20 years i) increased wheat yield by the new varieties; ii) continuous agriculture under no-till substituting crop-pasture rotation. The first imply increased N requirements; the second, reduced N supply from the soil. This scenario is not reflected by the database used to adjust best management practices to define the N fertilizer rates. While yield level categories proposed by Baetghen⁶ to define N fertilizer requirement at GS 3.0 include three yield categories lower than 3.5 Mg ha^-1 (2.5, 1.5 and <1.5), yield higher than 3.5 Mg ha^-1 are included in a single category. Our results show that, except under N_soil-Low scenarios (Fig. 5, TG2, TG4 and TG6), wheat yield would be assigned to “yield higher than 3.5 Mg ha^-1” category (Supplementary material 1). Furthermore, the mean Y_highest was 3 Mg higher than the limit proposed to the highest yield category (6.5 vs 3.5 Mg ha^-1, respectively, Table 3). These results confirm that N fertilizer decisions are taken following a scheme that is not reflecting the real wheat N requirements generated by new high wheat yield varieties. Although the Yg was reduced applying N fertilizer to seeding, GS 2.2 and GS 3.0, more than 0.6 Mg ha^-1 of wheat yield was lost due to N deficit at GS 3.3 (Fig. 5b and Table 3). We interpret the Yg attributed to low NNI at GS 3.3 (Fig. 5a) responds to sub-estimated N requirements to reach the actual attainable wheat yield (Y_highest).

Related to soil N supply capacity, two results must be remarked: i) 40% of experimental sites represent N_soil-Low scenarios; ii) assuming 30 kg of N to produce 1 Mg of grain wheat³⁶, soil N supply varied between 51 and 87 kg ha^-1, representing 26 to 45% of N required to Y_highest. While sites representing N_soil-High supplied around 45-65% of N required (Supplementary material 1). Although these soil N supply variability implied increased N fertilizer rates applied until GS 3.0, the Yg attributed to N deficit at GS 3.3 was mitigated but not suppressed (Table 3).

The NDC adjusted under current production conditions (Fig. 3) would be used to identify limited N conditions independently from growth phenological stage, allowing an effective diagnostic to monitoring N status from GS 2.2 to GS 6.5 in real time. This approach was proposed by Lemaire and others³⁷, as “new paradigms for crop mineral nutrition and fertilization towards sustainable agriculture”. In situ crop N diagnosis should help determine when additional N fertilization is required. It would be a new tool to improve crop N fertilization management.

Combining NDC and NNI concepts, we identify an NNI critical value at GS 3.3 to maximize wheat grain yield (Fig. 2b). The novelty is that using this function we can identify 74% of grain yield limited by N supply condition (Table 2). The critical NNI value at GS 3.3 was higher than 1 (NNI_critical = 1.24), suggesting that crop Nc to reach Y_max must be 24% higher than Nc to maximize DM at GS 3.3.

We adjust a new NDC (NDC_yield), but using only DM variability accumulated until GS 3.3. This NDC_yield is valid to identify grain wheat yield limited by N nutrition conditions only at GS 3.3 phenological stage. Contrasting two N rates applied at GS 3.3 (0 vs 50 kg ha^-1) in independently experiments, we identify around 80% of such conditions (Table 2), where grain yield was increased by an average of 0.6 Mg ha^-1 (data non showed).

While our research strategy does not permit N fertilizer rates recommendations (how much N), yield gap explained by crop N deficiency at GS 3.3 quantify how much grain yield is lost. This Yg would express differential response pattern to N fertilizer depending from the soil N supply capacity, affecting the N use efficiency⁷. Grain yield depletion in response to NNI<1 varied between 3 and 10% of Y_highest (N_soil-High or N_soil-Low, respectively, Fig. 5). Since our benchmark yield (Y_highest) varied from 5.46 to 7.68 Mg ha^-1 (Table 3), the Yg attributed to deficient crop N nutrition at GS 3.3 varied from 0 to 3.04 Mg ha^-1 and from 0 to 5.25 Mg ha^-1 under N_soil-High and N_soil-Low conditions, respectively.

The analysis suggests that N fertilizer management needs to be adjusted differentially when operating under variable soil N supply capacity. We hypothesize that the differential Yg responds to a progressive N release from the soil caused by increased temperature and soil water availability during the spring, where N_soil-High would improve N mineral release to crop growth.

To improve N diagnosis, it should also include the nitrogen to be mineralized during the crop growing season. For example, N potentially mineralizable has been proposed to adjust N fertilizer rates³⁸. This soil N supply capacity indicator could be a powerful tool to improve our N supply diagnosis to reduce both type I and Type II errors (Table 2). This concept was included as “high or low expected response to N fertilization” groups by Hoffman and others⁴. The Y_max obtained in both environments was similar (6.5 vs. 6.7 Mg ha^-1), which would indicate that N was the main limitation. Meanwhile, the existence of a RYg=0.1 even in NNI>NNI_critical for N_soil-Low conditions suggests the existence of additional limitations, either of N not satisfied with an accumulation of N above the NDC to GS 3.3, or related to other soil properties not directly related to the supply of N. This concept would be equivalent to the one managed by Ernst and others⁷, who attribute it to deterioration of physical properties of the soil that modify the efficiency of use of N. Also, other nutrients may not be limiting at reduced yield levels when the crop is deficient in N, but they become limiting at higher yield levels, made possible by better nitrogen nutrition of the plant³¹.

Our results contribute to reducing the uncertainty of the prognosis based on soil N supply indicator only. Monitoring crop N status would reduce the risk of yield reduction, avoiding the current tendency to overfertilize because of the great uncertainty for forecasting N fertilizer requirements.

5. Conclusions

Our study quantified a wheat yield gap (Yg) attributed to limited crop N nutrition at GS 3.3, yet under the best management practices. This Yg increased under low soil N supply conditions (N_soil-Low). The nitrogen dilution curve adjusted under local conditions has two benefits: i) it permits permanent N diagnosis independently form crop growth phenological stage; and ii) it allows to derive the nitrogen nutrition index (NNI) critical value at GS 3.3 to maximize wheat grain yield. This critical NNI value was an effective tool diagnosing the increased N demand imposed by current attainable yields.